Trigonometri Formülleri

Trigonometrik Formüller

Altı temel trigonometrik fonksiyon bir dik üçgen yardımıyla kolaylıkla tanımlanabilir. Bu altı temel trigonometrik fonksiyon sırasıyla sinüs, kosinüs, tanjant, kotanjant, sekant ve kosekanttır. İngilizce adlarının ilk üç harfi kullanılarak (kosekant hariç) kısaltılmışlardır.

1. sin A = a / c

2. cos A = b / c

3. tan A = a / b

4. cot A = b / a

5. sec A = c / b

6. csc A = c / a

1. Tek-Çift Fonksiyonlar

1. sin (- x) = - sin x

2. cos (- x) = cos x

3. tan (- x) = - tan x

4. cot (- x) = - cot x

5. sec (- x) = sec x

6. csc (- x) = - csc x

Eğer f (- x) = f (x) ise fonksiyon çift, f (- x) = - f (x) ise fonksiyon tektir. Buna göre kosinüs ve sekant fonksiyonları çift fonksiyon olur iken; sinüs, tanjant, kotanjant ve kosekant fonksiyonları ise tek fonksiyon olur.

2. Aralarındaki İlişkiler

1. sec x = 1 / cos x

2. csc x = 1 / sin x

3. tan x = sin x / cos x

4. cot x = cos x / sin x

5. tan x . cot x = 1

3. Aralarındaki Pisagorik İlişkiler

Yukarıdaki üçgeni kullanarak ve Pisagor Teoreminin de yardımıyla aşağıdaki eşitlikleri elde edebiliriz.

1. sin² x + cos² x = 1

2. sec² x = 1 + tan² x

3. csc² x = 1 + cot² x

4. Toplam ve Fark Formülleri

Trigonometrik değerini bildiğimiz iki açının toplam veya farkının trigonometrik değerini hesaplamak için kullanacağımız formüllere toplam ve fark formülleri denir. Bunlar şunlardır;

1. sin (x + y) = sin x . cos y + cos x . sin y

2. sin (x - y) = sin x . cos y - cos x . sin y

3. cos (x + y) = cos x . cos y - sin x . sin y

4. cos (x - y) = cos x . cos y + sin x . sin y

5. tan (x + y) = (tan x + tan y) / (1 - tan x . tan y)

6. tan (x - y) = (tan x - tan y) / (1 + tan x . tan y)

7. cot (x + y) = (cot x . cot y - 1) / (cot x + cot y)

8. cot (x - y) = (cot x . cot y + 1) / (cot x - cot y)

5. Çift ve Yarım Açı Formülleri

Trigonometrik değeri bilinen bir açının iki katının veya yarısının trigonometrik değerini hesaplamak için kullanılan formüllere iki kat açı (çift açı) veya yarım açı formülleri denir. Bunlar şunlardır;

1. sin 2x = 2 . sin x . cos x

2. cos 2x = cos² x - sin² x = 2 . cos² x - 1 = 1 - 2 . sin² x

3. tan 2x = 2 . tan x / (1 - tan² x)

4. cot 2x = (cot² x - 1) / 2 . cot x

5. sin x/2 = ± √(1 - cos x) / 2

6. cos x/2 = ± √(1 + cos x) / 2

7. tan x/2 = ± √(1 - cos x) / (1 + cos x) = sin x / (1 + cos x) = (1 - cos x) / sin x

8. cot x/2 = ± √(1 + cos x) / (1 - cos x) = (1 + cos x) / sin x = sin x / (1 - cos x)

9. sin² x = 1 / 2 . (1 - cos 2x)

10. cos² x = 1 / 2 . (1 + cos 2x)

11. tan² x = (1 - cos 2x) / (1 + cos 2x)

12. cot² x = (1 + cos 2x) / (1 - cos 2x)

6. Dönüşüm Formülleri

Toplam ve fark şeklindeki trigonometrik ifadeleri çarpım şekline dönüştürmeye yarayan, toplam ve fark formüllerinden yola çıkarak (yararlanarak) elde edilen formüllerdir. Bunlar şunlardır;

1. sin x + sin y = 2 . sin (x + y)/2 . cos (x - y)/2

2. cos x + cos y = 2 . cos (x + y)/2 . cos (x - y)/2

3. tan x + tan y = sin (x + y) / cos x . cos y

4. cot x + cot y = sin (x + y) / sin x . sin y

5. sin x - sin y = 2 . sin (x - y)/2 . cos (x + y)/2

6. cos x - cos y = -2 . sin (x + y)/2 . sin (x - y)/2

7. tan x - tan y = sin (x - y) / cos x . cos y

8. cot x - cot y = -sin (x - y) / sin x . sin y

7. Ters Dönüşüm Formülleri

Çarpım şeklindeki trigonometrik ifadeleri toplam ve fark şekline dönüştürmeye yarayan, toplam ve fark formüllerinden yola çıkarak (yararlanarak) elde edilen formüllerdir. Bunlar şunlardır;

1. sin x . sin y = -1 / 2 . [cos (x + y) - cos (x - y)]

2. cos x . cos y = 1 / 2 . [cos (x + y) + cos (x - y)]

3. sin x . cos y = 1 / 2 . [sin (x + y) + sin (x - y)]

4. tan x . tan y = (tan x + tan y) / (cot x + cot y)

5. cot x . cot y = (cot x + cot y) / (tan x + tan y)

6. tan x . cot y = [sin (x + y) + sin (x - y)] / [sin (x + y) - sin (x - y)]

8. Diğer Özellikleri

1. sin (90 - x) = cos x

2. cos (90 - x) = sin x

3. tan (90 - x) = cot x

4. cot (90 - x) = tan x

5. sec (90 - x) = csc x

6. csc (90 - x) = sec x

9. Sonsuz Seri Şeklindeki Açılımları

Trigonometrik ifadeleri (fonksiyonları) sonsuz bir seri şeklinde açabiliriz. sin x ve cos x fonksiyonlarının soru şeklindeki açılımları aşağıdaki gibidir.

1. sin x = x - x³ / 3! + x⁵ / 5! - x⁷ / 7! + . . .

2. cos x = 1 - x² / 2! + x⁴ / 4! - x⁶ / 6! + . . .

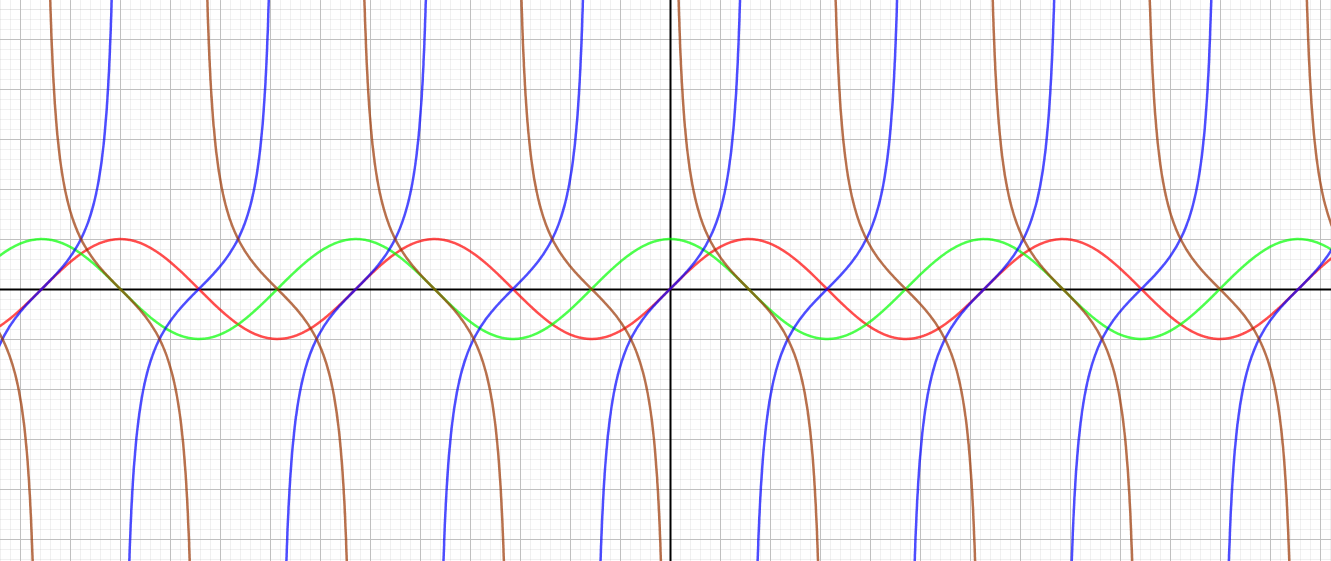
Trigonometrik Fonksiyonların Grafikleri

sinüs (kırmızı), kosinüs (yeşil), tanjant (mavi) ve kotanjant (kahverengi) fonksiyonlarının grafikleri aşağıdaki gibidir.

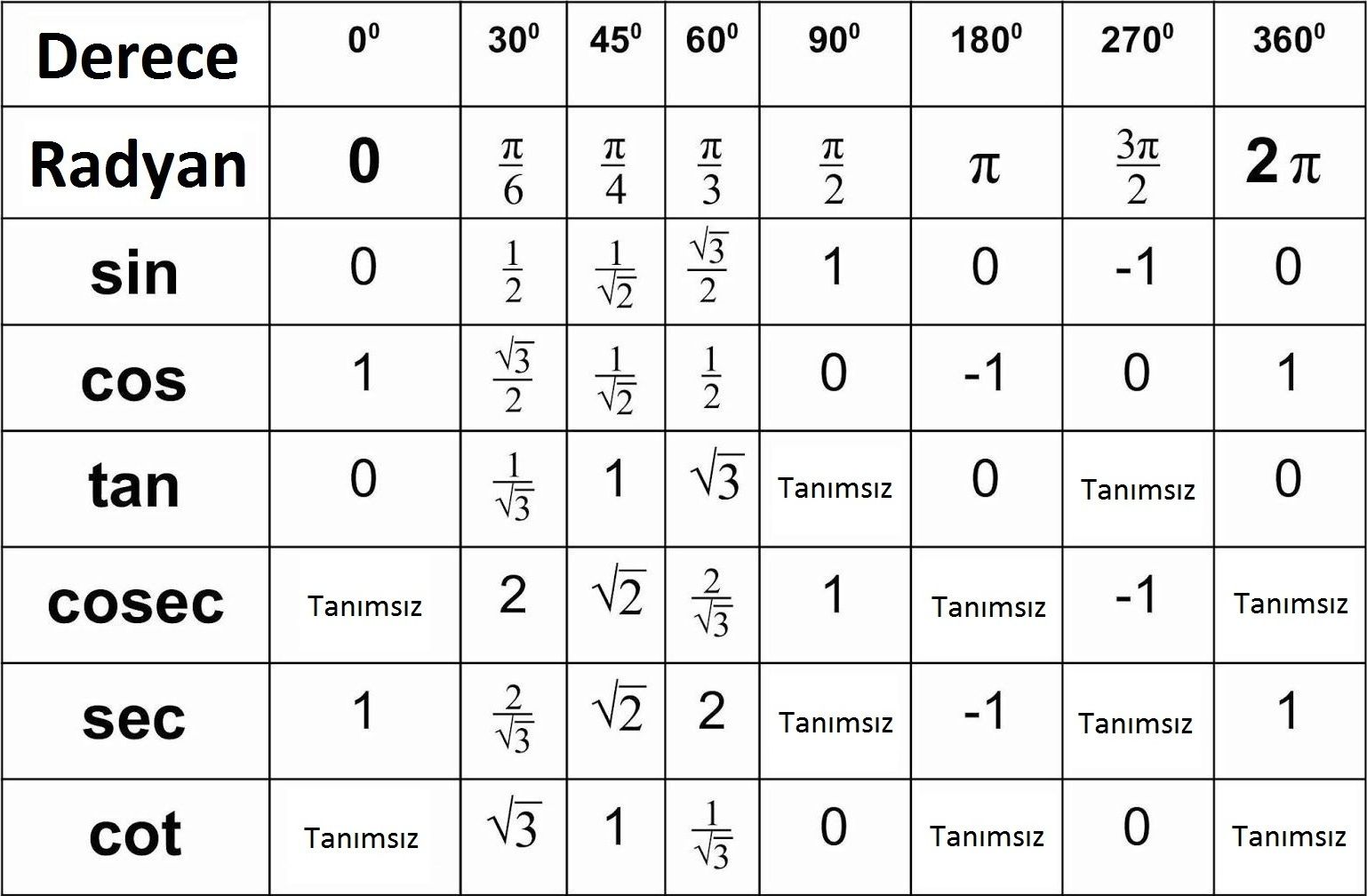
Trigonometri Tablosu

Önemli trigonometrik değerlerin derece ve radyan cinsinden karşılıkları aşağıdaki tabloda verilmiştir.