Sinx Fonksiyonunun Türevi Neden Cosx Fonksiyonudur

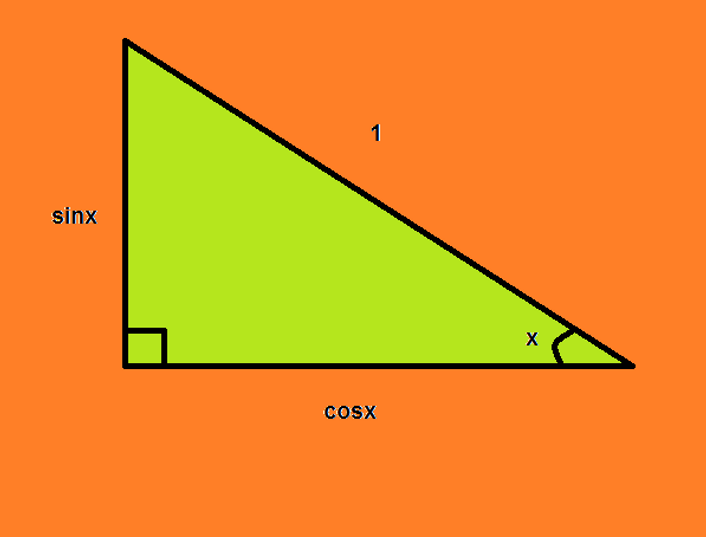
Aşağıya hipotenüsü 1 birim olan bir dik üçgen çizelim.

sinx² + cosx² = 1²

sinx² + cosx² = 1

(sinx² + cosx²)’ = (1)’ (eşitliğin iki tarafının da türevini aldık)

(sinx²)’ + (cosx²)’ = 0 (sabit sayısının türevi sıfırdır)

2.sinx.sinx’ + 2.cosx.cosx’ = 0 olur.

2.(sinx.sinx’ + cosx.cosx’) = 0

sinx.sinx’ + cosx.cosx’ = 0 ise

sinx.sinx’ = -cosx.cosx’ (1. Denklem)

veya

cosx.cosx’ = -sinx.sinx’ (2. Denklem) olur.

Buradan

1. Denklemde sinx’ = -cosx ve 2. Denklemde sinx’ = cosx olur.

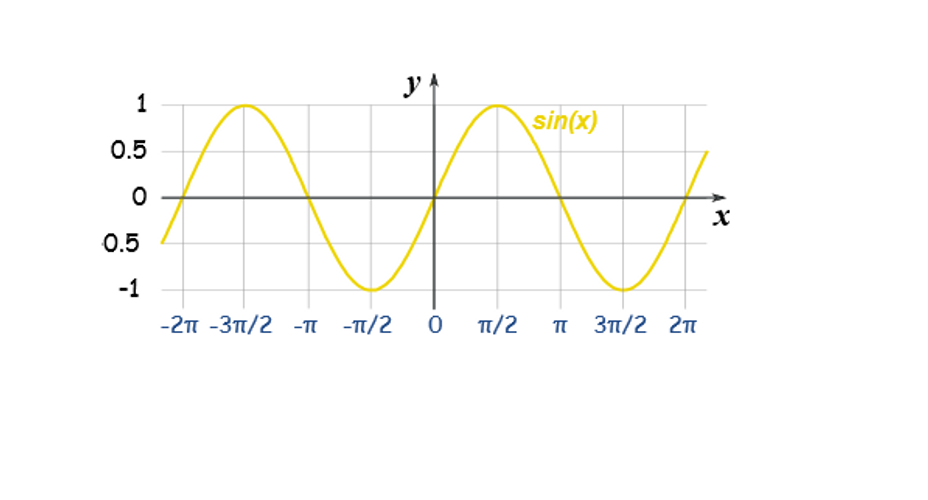
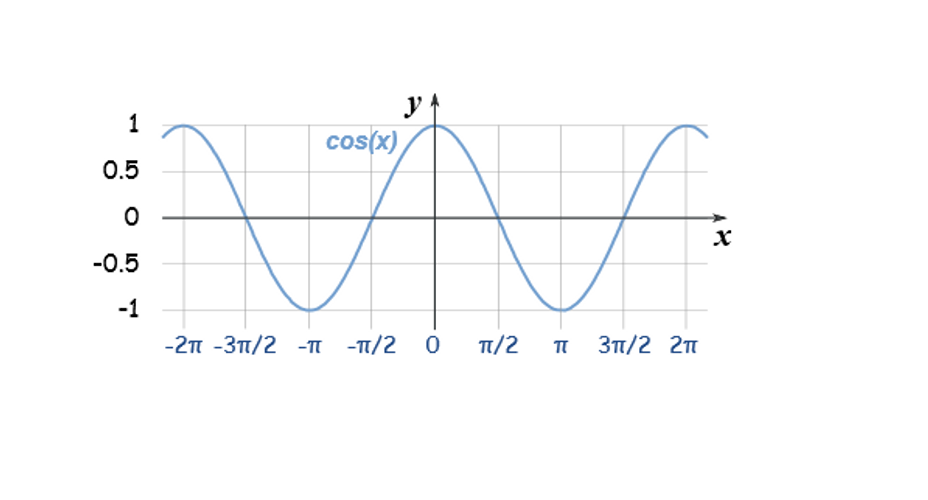
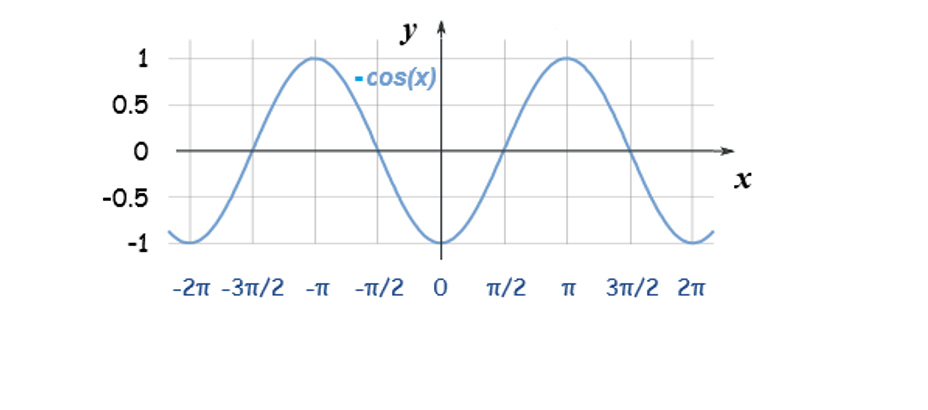
Aşağıya sinx, cosx ve –cosx fonksiyonunun grafiğini çizelim.

Sinx fonksiyonunun grafiğini incelediğimizde 0 ile π/2 aralığında artan bir fonksiyon ve π/2 ile π aralığında ise azalan bir fonksiyon olduğunu görürüz. Buradan 0 ile π/2 aralığında sinx fonksiyonunun üzerinden seçilen bir noktanın teğetinin eğiminin sıfırdan büyük (türevin pozitif) ve π/2 ile π aralığında seçilen bir noktanın teğetinin eğiminin ise sıfırdan küçük (türevin negatif) olduğunu görürüz.

Cosx ve –cosx fonksiyonunu ayrı ayrı incelediğimizde ise cosx fonksiyonunun 0 ile π/2 aralığında sıfırdan büyük (pozitif) değerler ve π/2 ile π aralığında ise sıfırdan küçük (negatif) değerler aldığını görürüz. -Cosx fonksiyonunun ise 0 ile π/2 aralığında sıfırdan küçük (negatif) değerler ve π/2 ile π aralığında ise sıfırdan büyük (pozitif) değerler aldığını görürüz. Sinx fonksiyonunun 0 ile π/2 aralığında türevinin sıfırdan büyük ve π/2 ile π aralığında ise türevinin sıfırdan küçük olduğunu Yukarıda daha önce açıklamıştık o zaman bu koşula cosx fonksiyonu uyduğuna göre sinx fonksiyonunun türevi cosx fonksiyonudur.

Sinx' = Cosx'dir.