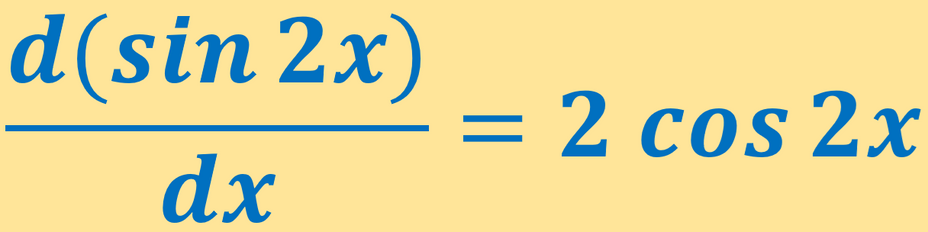Sin 2x'in türevi 2.cos 2x'tir.
Sin 2x'in Türevi Nedir ? Sin 2x'in türevi 2.cos 2x'tir.
( s in 2 x ) ′ = 2. cos 2 x
d x d ( s in 2 x ) = 2. cos 2 x
Sin 2x'in Türevinin İspatı 1. Yol f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) ( s in 2 x ) ′ = h → 0 lim h s in 2 ( x + h ) − s in 2 x ( s in 2 x ) ′ = h → 0 lim h s in ( 2 x + 2 h ) − s in 2 x s in ( p + q ) = s in p . cos q + cos p . s in q ( s in 2 x ) ′ = h → 0 lim h s in 2 x . cos 2 h + cos 2 x . s in 2 h − s in 2 x ( s in 2 x ) ′ = h → 0 lim h s in 2 x . cos 2 h − s in 2 x + cos 2 x . s in 2 h ( s in 2 x ) ′ = h → 0 lim h s in 2 x . ( cos 2 h − 1 ) + cos 2 x . s in 2 h ( s in 2 x ) ′ = h → 0 lim 2. h 2. [ s in 2 x . ( cos 2 h − 1 ) + cos 2 x . s in 2 h ] ( s in 2 x ) ′ = 2. h → 0 lim 2 h s in 2 x . ( cos 2 h − 1 ) + cos 2 x . s in 2 h ( s in 2 x ) ′ = 2. h → 0 lim [ 2 h s in 2 x . ( cos 2 h − 1 ) + 2 h cos 2 x . s in 2 h ] ( s in 2 x ) ′ = 2. h → 0 lim 2 h s in 2 x . ( cos 2 h − 1 ) + 2. h → 0 lim 2 h cos 2 x . s in 2 h ( s in 2 x ) ′ = 2. s in 2 x . h → 0 lim 2 h cos 2 h − 1 + 2. cos 2 x . h → 0 lim 2 h s in 2 h
h → 0 ( 2 h = h )
( s in 2 x ) ′ = 2. s in 2 x . h → 0 lim h cos h − 1 + 2. cos 2 x . h → 0 lim h s in h
t → 0 l i m t s in t = 1 t → 0 l i m t cos t − 1 = 0
( s in 2 x ) ′ = 2. s in 2 x .0 + 2. cos 2 x .1
( s in 2 x ) ′ = 0 + 2. cos 2 x
( s in 2 x ) ′ = 2. cos 2 x
2. Yol f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) ( s in 2 x ) ′ = h → 0 lim h s in 2 ( x + h ) − s in 2 x ( s in 2 x ) ′ = h → 0 lim h s in ( 2 x + 2 h ) − s in 2 x s in p − s in q = 2. s in 2 p − q . cos 2 p + q ( s in 2 x ) ′ = h → 0 lim h 2. s in 2 2 x + 2 h − 2 x . cos 2 2 x + 2 h + 2 x ( s in 2 x ) ′ = h → 0 lim h 2. s in 2 2 h . cos 2 4 x + 2 h ( s in 2 x ) ′ = 2. h → 0 lim h s in 2 2 h . cos 2 4 x + 2 h ( s in 2 x ) ′ = 2. h → 0 lim h s in 2 2 . h . cos 2 2 . ( 2 x + h ) ( s in 2 x ) ′ = 2. h → 0 lim h s in h . cos ( 2 x + h ) ( s in 2 x ) ′ = 2. h → 0 lim [ h s in h . cos ( 2 x + h )] ( s in 2 x ) ′ = 2. h → 0 lim h s in h . h → 0 lim cos ( 2 x + h ) ( s in 2 x ) ′ = 2.1. cos ( 2 x + 0 )
( s in 2 x ) ′ = 2.1. cos 2 x
( s in 2 x ) ′ = 2. cos 2 x
3. Yol s in 2 x = 2 x − 3 ! ( 2 x ) 3 + 5 ! ( 2 x ) 5 − 7 ! ( 2 x ) 7 + 9 ! ( 2 x ) 9 − ...
cos 2 x = 1 − 2 ! ( 2 x ) 2 + 4 ! ( 2 x ) 4 − 6 ! ( 2 x ) 6 + 8 ! ( 2 x ) 8 − ...
s in 2 x = 2 x − 3 ! ( 2 x ) 3 + 5 ! ( 2 x ) 5 − 7 ! ( 2 x ) 7 + 9 ! ( 2 x ) 9 − ...
( s in 2 x ) ′ = [ 2 x − 3 ! ( 2 x ) 3 + 5 ! ( 2 x ) 5 − 7 ! ( 2 x ) 7 + 9 ! ( 2 x ) 9 − ... ] ′
( s in 2 x ) ′ = ( 2 x ) ′ − [ 3 ! ( 2 x ) 3 ] ′ + [ 5 ! ( 2 x ) 5 ] ′ − [ 7 ! ( 2 x ) 7 ] ′ + [ 9 ! ( 2 x ) 9 ] ′ − ...
( s in 2 x ) ′ = 2 − 3 ! 3. ( 2 x ) 2 . ( 2 x ) ′ + 5 ! 5. ( 2 x ) 4 . ( 2 x ) ′ − 7 ! 7. ( 2 x ) 6 . ( 2 x ) ′ + 9 ! 9. ( 2 x ) 8 . ( 2 x ) ′ − ...
( s in 2 x ) ′ = 2 − 3 ! 3. ( 2 x ) 2 .2 + 5 ! 5. ( 2 x ) 4 .2 − 7 ! 7. ( 2 x ) 6 .2 + 9 ! 9. ( 2 x ) 8 .2 − ...
( s in 2 x ) ′ = 2 − 3 .2 ! 3 . ( 2 x ) 2 .2 + 5 .4 ! 5 . ( 2 x ) 4 .2 − 7 .6 ! 7 . ( 2 x ) 6 .2 + 9 .8 ! 9 . ( 2 x ) 8 .2 − ...
( s in 2 x ) ′ = 2 − 2 ! ( 2 x ) 2 .2 + 4 ! ( 2 x ) 4 .2 − 6 ! ( 2 x ) 6 .2 + 8 ! ( 2 x ) 8 .2 − ...
( s in 2 x ) ′ = 2. [ 1 − 2 ! ( 2 x ) 2 + 4 ! ( 2 x ) 4 − 6 ! ( 2 x ) 6 + 8 ! ( 2 x ) 8 − ... ]
( s in 2 x ) ′ = 2. cos 2 x