Sinüs Teoremi Kosinüs Teoremi (Sinüs ve Kosinüs Teoremleri)

Pow
İki Kenarı ve Bir Açısı Bilinen Bir Üçgenin Alanını Bulma İki kenarı ve bu iki kenarının arasındaki açının ölçüsü bilinen herhangi bir üçgenin alanını aşağıdaki
İki Kenarı ve Bir Açısı Bilinen Bir Üçgenin Alanını Bulma
İki kenarı ve bu iki kenarının arasındaki açının ölçüsü bilinen herhangi bir üçgenin alanını aşağıdaki şekildeki gibi hesaplayabiliriz. İki kenarı ve bu iki kenarının arasındaki açının ölçüsü bilinen aşağıdaki ABC üçgeninin alanı;
A(ABC) = 1 / 2 . b . c . sinA'dır.
İspat
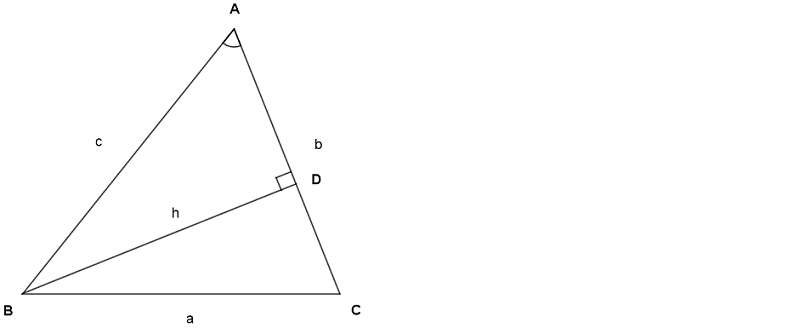
Yukarıdaki ABC üçgenin alanı;
A (ABC) = (b . h) / 2'dir.
ABD dik üçgeninde sinA = h / c olur.
h / c = sinA ise h = c . sinA olur.
Yukarıdaki alan formülünde h gördüğümüz yere c . sinA yazalım.
A (ABC) = (b . c . sinA ) / 2 = 1 / 2 . b . c . sinA olur.
Aynı formülü üçgenin diğer kenarı ve açıları için de uygularsak;
A (ABC) = 1 / 2 . a . c . sinB
A (ABC) = 1 / 2 . a . b . sinC olur.
Sinüs Teoremi
Sinüs teoremine göre; bir üçgenin herhangi bir kenar ile o kenarının karşısında kalan açının sinüsünün oranı diğer kenarları ile o kenarlarının karşısında kalan açıların sinüslerinin oranına eşittir. Bu oran aynı zamanda üçgenin çevrel çemberinin çapı olan 2r'ye eşittir.
Herhangi bir ABC üçgeninde a, b ve c üçgenin kenar uzunlukları, A, B ve C üçgenin iç açıları ve r de çevrel çemberin yarıçapı olmak üzere sinüs teoremine göre aralarında aşağıdaki şekildeki gibi bir bağıntı vardır.
1. sinA / a = sinB / b = sinC / c
2. a / sinA = b / sinB = c / sinC = 2 . r
Sinüs Teoreminin İspatı
1. sinA / a = sinB / b = sinC / c'nin İspatı
1 / 2 . b . c . sinA = 1 / 2 . a . c . sinB = 1 / 2 . a . b . sinC
b . c . sinA = a . c . sinB = a . b . sinC
b . c . sinA / a . b . c = a . c . sinB / a . b . c = a . b . sinC / a . b . c
sinA / a = sinB / b = sinC / c veya a / sinA = b / sinB = c / sinC
2. a / sinA = b / sinB = c / sinC = 2 . r'nin İspatı
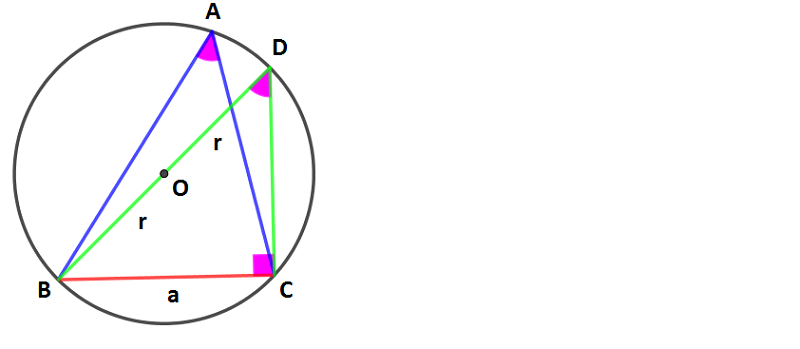
Yukarıda O merkezli r yarıçaplı bir çevrel çember içerisine çizilmiş olan bir ABC üçgeni görmektesiniz. Bir çemberde aynı yayı gören çevre açıların ölçüleri birbirine eşit olacağı için A açısının ölçüsü ile D açısının ölçüsü birbirine eşittir. Bir çember de çapı gören çevre açının ölçüsü 90° olacağı için C açısının ölçüsü de doksan derece olur.
m (A) = m (D)
m (C) = 90
sinD = sinA = a / 2r
sinA = a / 2r
1 / sinA = 2r / a
a / sinA = 2r olur.
Aynı formülü çevrel çember içerisindeki üçgenin diğer kenarı ve açıları için de uygularsak;
b / sinB = 2r
c / sinC = 2r
a / sinA = b / sinB = c / sinC = 2r olur.
2. Kosinüs Teoremi
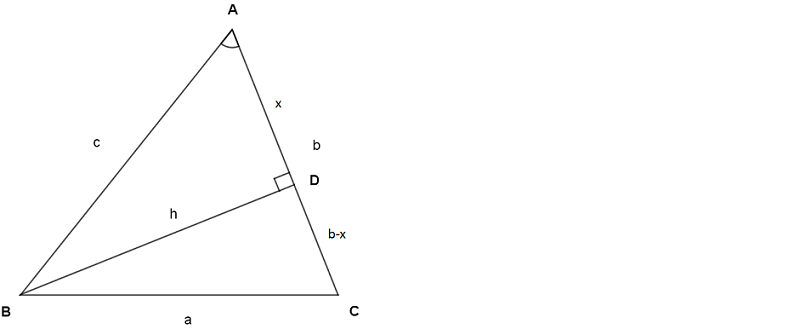
İki kenarı ve bu iki kenarının arasındaki açının değeri bilinen herhangi bir ABC üçgeninin üçüncü kenarını aşağıdaki şekildeki gibi bulabiliriz.
İki kenarı ve bu iki kenarının arasındaki açının değeri bilinen aşağıdaki ABC üçgeninin üçüncü kenarı;
a² = b² + c² - 2 . b . c . cosA'dır.
Kosinüs Teoreminin İspatı
Bu eşitliğin ispatını aşağıdaki şekildeki gibi yapabiliriz.
Yukarıdaki şekildeki ABD ve DBC üçgenleri birer dik üçgendir.
ABD dik üçgeninde Pisagor teoremine göre;
c² = x² + h²
DBC dik üçgeninde Pisagor teoremine göre;
a² = (b - x)² + h²
a² = b² - 2 . b . x + x² + h²
a² = b² - 2 . b . x + c²
ABD dik üçgeninde cosA = x / c'dir.
x / c = cosA
x = c . cosA
a² = b² - 2 . b . x + c² eşitliğindeki x'in yerine yukarıda bulduğumuz değeri yazalım.
a² = b² - 2 . b . c . cosA + c²
a² = b² + c² - 2 . b . c . cosA olur.
Aynı formülü üçgenin diğer kenarı ve açıları için de uygularsak;
b² = a² + c² - 2 . a . c . cosB
c² = a² + b² - 2 . a . b . cosC olur.
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.