Sinüs Teoremi

Pow
Sinüs Teoremi Nedir? Bir ABC üçgeninde üçgenin herhangi bir kenar ile bu kenarın karşısındaki açının sinüsünün oranı diğer kenarları ile bu kenarlarının karşısı
Sinüs Teoremi Nedir?
Bir ABC üçgeninde üçgenin herhangi bir kenar ile bu kenarın karşısındaki açının sinüsünün oranı diğer kenarları ile bu kenarlarının karşısındaki açıların sinüslerinin oranına eşittir. Bu sabit oranın değeri aynı zamanda üçgenin çevrel çemberinin çapına eşittir. Buna sinüs teoremi, sinüs yasası veya sinüs kanunu denir.
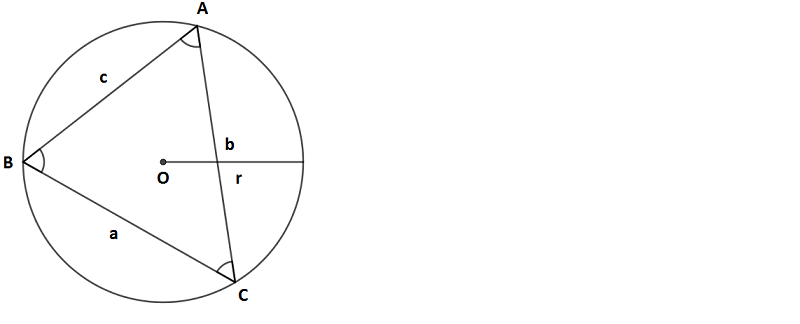
Yukarıdaki şekildeki O merkezli r yarıçaplı çember, ABC üçgeninin bir çevrel çemberidir. Buna göre;
a / sinA = b / sinB = c / sinC = 2r olur.
İspat
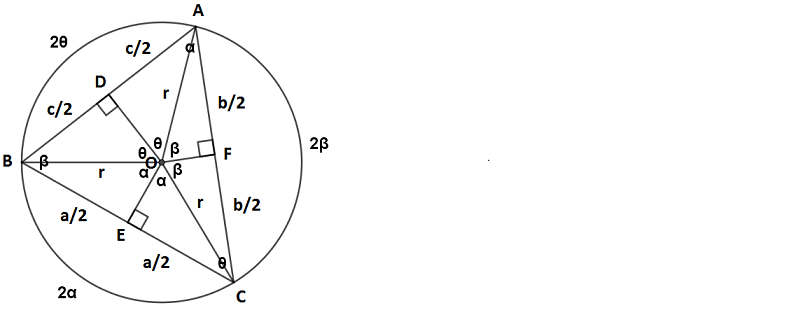
Aşağıdaki şekildeki O merkezli r yarıçaplı çember, ABC üçgeninin bir çevrel çemberidir. Bir çemberde çevre açının ölçüsü gördüğü yayın ölçüsünün yarısına eşit iken; merkez açının ölçüsü ise gördüğü yayın ölçüsüne eşittir. İkiz kenar bir üçgende eşit olmayan üçüncü kenara inilen bir dikme, inilen köşedeki açıyı ve inilen kenarı iki eşit parçaya böler. Şimdi bu bilgilerden ve üçgenlerdeki benzerlik kurallarından da faydalanarak yukarıda vermiş olduğumuz formülü aşağıda ispatlamaya çalışalım.
OEB veya OEC Üçgeni için;
a/2 / r = sinα
a/2r = sinα
a = 2r . sinα
a / sinα = 2r . sinα / sinα
a / sinα = 2r olur.
OFA veya OFC Üçgeni için;
b/2 / r = sinβ
b/2r = sinβ
b = 2r . sinβ
b / sinβ = 2r . sinβ / sinβ
b / sinβ = 2r olur.
ODA veya ODB Üçgeni için;
c/2 / r = sinθ
c/2r = sinθ
c = 2r . sinθ
c / sinθ = 2r . sinθ / sinθ
c / sinθ = 2r olur.
a / sinα = 2r
b / sinβ = 2r ise a / sinα = b / sinβ = c / sinθ = 2r olur.
c / sinθ = 2r
İki Kenarı ve Bir Açısı Bilinen Bir Üçgenin Alanını Hesaplama
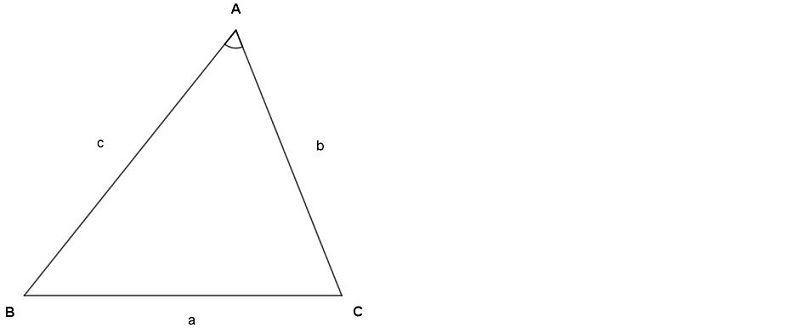
İki kenarı ve bu iki kenarının arasındaki açısının ölçüsünü bildiğimiz yukarıdaki ABC üçgeninin alanını aşağıdaki şekildeki gibi hesaplayabiliriz.
A(ABC) = 1 / 2 . b . c . sinA'dır.
İspat
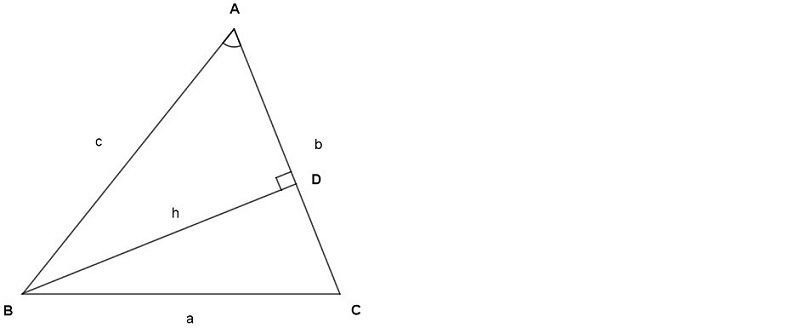
Yukarıdaki ABC üçgenin alanı;
A (ABC) = (b . h) / 2'dir.
ABD dik üçgeninde sinA = h / c olur.
h / c = sinA ise h = c . sinA olur.
Yukarıdaki alan formülünde h gördüğümüz yere c . sinA yazalım.
A (ABC) = (b . c . sinA ) / 2 = 1 / 2 . b . c . sinA olur.
Aynı formülü üçgenin diğer kenarları ve açıları için de uygularsak;
A (ABC) = 1 / 2 . a . c . sinB
A (ABC) = 1 / 2 . a . b . sinC olur.
1 / 2 . b . c . sinA = 1 / 2 . a . c . sinB = 1 / 2 . a . b . sinC
b . c . sinA = a . c . sinB = a . b . sinC
b . c . sinA / a . b . c = a . c . sinB / a . b . c = a . b . sinC / a . b . c
sinA / a = sinB / b = sinC / c veya a / sinA = b / sinB = c / sinC olur.
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.