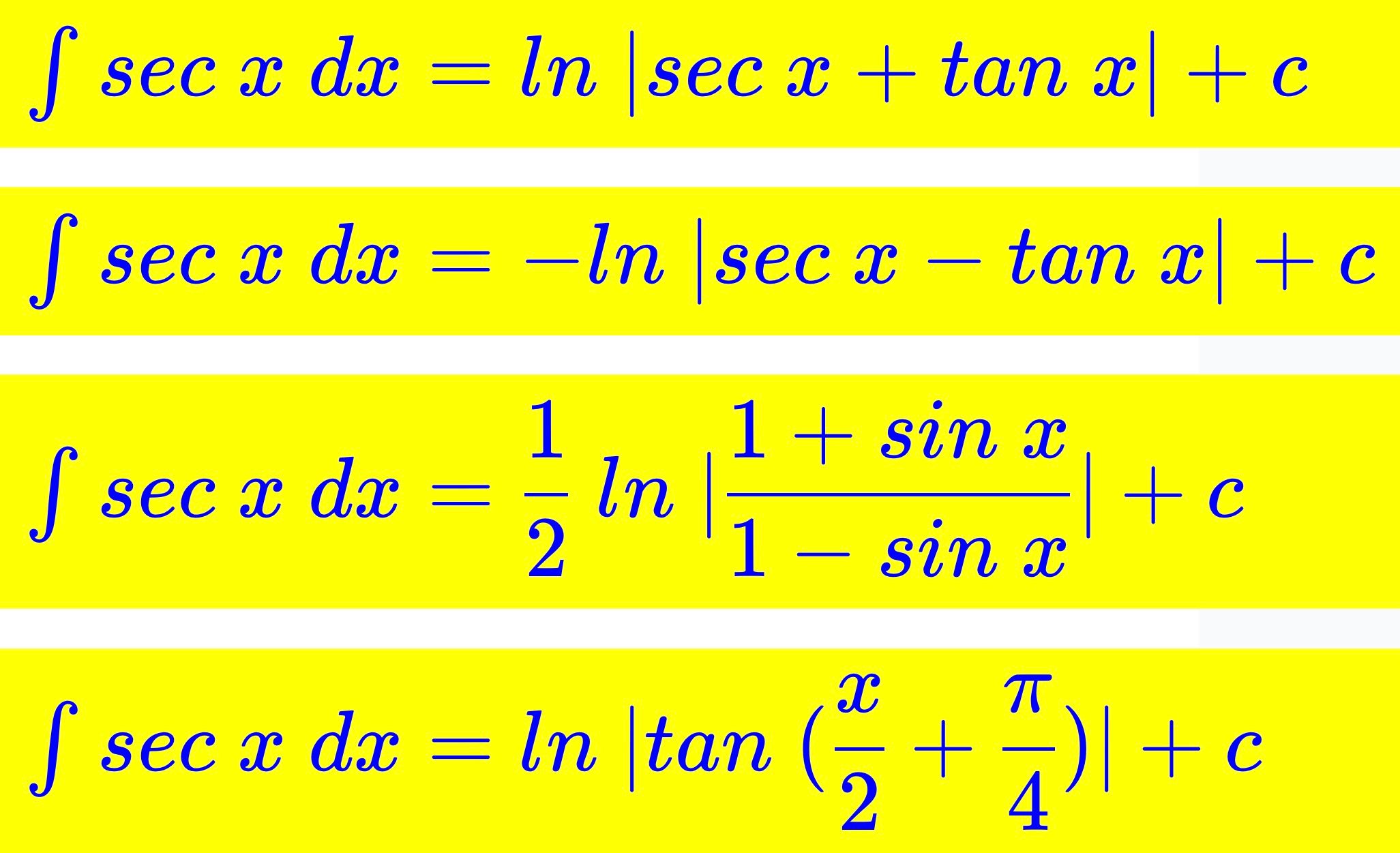Sec x'in integrali ln |sec x+tan x|+c'dir.
Sec x'in İntegrali Nedir ? Sec x'in integrali ln |sec x+tan x|+c'dir.
∫ sec x d x = l n ∣ sec x + t an x ∣ + c
∫ sec x d x = − l n ∣ sec x − t an x ∣ + c
∫ sec x d x = 2 1 l n ∣ 1 − s in x 1 + s in x ∣ + c
∫ sec x d x = l n ∣ t an ( 2 x + 4 π ) ∣ + c
Sec x'in İntegralini Bulma ∫ sec x d x = ∫ sec x + t an x ( sec x + t an x ) . sec x d x
∫ sec x d x = ∫ sec x + t an x sec x . sec x d x + sec x . t an x d x
∫ sec x d x = ∫ sec x + t an x se c 2 x d x + sec x . t an x d x
∫ sec x d x = ∫ sec x + t an x ( se c 2 x + sec x . t an x ) d x
sec x + t an x = u
d ( sec x + t an x ) = d ( u )
d [ f ( x )] = f ′ ( x ) d x ( sec x + t an x ) ′ d x = d u
( sec x ) ′ d x + ( t an x ) ′ d x = d u
( sec x ) ′ = sec x . t an x ( t an x ) ′ = se c 2 x sec x . t an x d x + se c 2 x d x = d u
( sec x . t an x + se c 2 x ) d x = d u
∫ sec x d x = ∫ u d u
∫ x d x = l n ∣ x ∣ + c ∫ sec x d x = l n ∣ u ∣ + c
∫ sec x d x = l n ∣ sec x + t an x ∣ + c
sec x = cos x 1 t an x = cos x s in x ∫ sec x d x = l n ∣ cos x 1 + cos x s in x ∣ + c
∫ sec x d x = l n ∣ cos x 1 + s in x ∣ + c
∫ sec x d x = l n ∣ ( 1 − s in x ) . cos x ( 1 − s in x ) . ( 1 + s in x ) ∣ + c
∫ sec x d x = l n ∣ ( 1 − s in x ) . cos x 1 − s i n 2 x ∣ + c
co s 2 x = 1 − s i n 2 x ∫ sec x d x = l n ∣ ( 1 − s in x ) . cos x co s 2 x cos x ∣ + c ∫ sec x d x = l n ∣ 1 − s in x cos x ∣ + c ∫ sec x d x = l n ∣ ( cos x 1 − s in x ) − 1 ∣ + c ∫ sec x d x = l n ∣ ( cos x 1 − s in x ) ∣ − 1 + c ∫ sec x d x = − l n ∣ ( cos x 1 − s in x ) ∣ + c ∫ sec x d x = − l n ∣ cos x 1 − cos x s in x ∣ + c
∫ sec x d x = − l n ∣ sec x − t an x ∣ + c
∫ sec x d x = l n ∣ sec x + t an x ∣ + c
∫ sec x d x = l n ∣ cos x 1 + cos x s in x ∣ + c
∫ sec x d x = l n ∣ cos x 1 + s in x ∣ + c
cos x = 1 − s i n 2 x ∫ sec x d x = l n ∣ 1 − s i n 2 x ( 1 + s in x ) 2 ∣ + c ∫ sec x d x = l n ∣ ( 1 − s in x ) . ( 1 + s in x ) ( 1 + s in x ) . ( 1 + s in x ) ∣ + c ∫ sec x d x = l n ∣ ( 1 − s in x ) . ( 1 + s in x ) ( 1 + s in x ) . ( 1 + s in x ) ∣ + c ∫ sec x d x = l n ∣ 1 − s in x 1 + s in x ∣ + c ∫ sec x d x = l n ∣ ( 1 − s in x 1 + s in x ) 2 1 ∣ + c ∫ sec x d x = l n ∣ 1 − s in x 1 + s in x ∣ 2 1 + c ∫ sec x d x = 2 1 l n ∣ 1 − s in x 1 + s in x ∣ + c
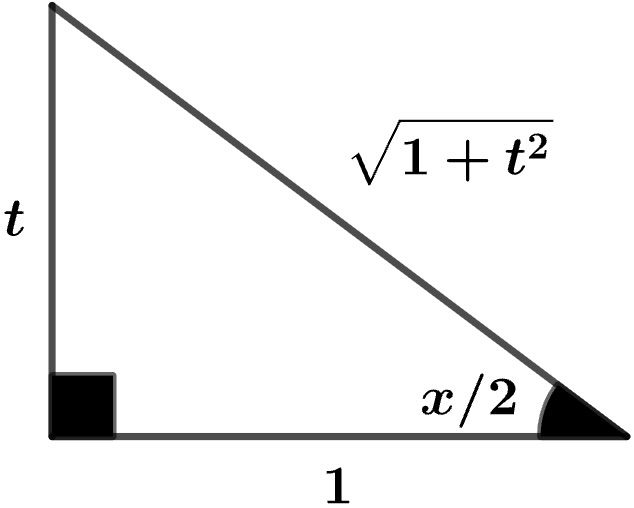
t an 2 x = t
s in 2 x = 1 + t 2 t
cos 2 x = 1 + t 2 1
s in 2 x = 2. s in x . cos x
∫ sec x d x = l n ∣ 1 − 2. s in 2 x . cos 2 x 1 + 2. s in 2 x . cos 2 x ∣ + c
∫ sec x d x = l n ∣ 1 − 2. 1 + t 2 t . 1 + t 2 1 1 + 2. 1 + t 2 t . 1 + t 2 1 ∣ + c
∫ sec x d x = l n ∣ 1 − 1 + t 2 . 1 + t 2 2. t .1 1 + 1 + t 2 . 1 + t 2 2. t .1 ∣ + c
∫ sec x d x = l n ∣ 1 − ( 1 + t 2 ) . ( 1 + t 2 ) 2. t 1 + ( 1 + t 2 ) . ( 1 + t 2 ) 2. t ∣ + c
∫ sec x d x = l n ∣ 1 − ( 1 + t 2 ) 2 2. t 1 + ( 1 + t 2 ) 2 2. t ∣ + c
∫ sec x d x = l n ∣ 1 − 1 + t 2 2. t 1 + 1 + t 2 2. t ∣ + c
∫ sec x d x = l n ∣ 1 + t 2 1 + t 2 − 2. t 1 + t 2 1 + t 2 + 2. t ∣ + c
∫ sec x d x = l n ∣ 1 + t 2 1 + t 2 − 2. t 1 + t 2 1 + t 2 + 2. t ∣ + c
∫ sec x d x = l n ∣ 1 + t 2 − 2. t 1 + t 2 + 2. t ∣ + c
∫ sec x d x = l n ∣ 1 − 2. t + t 2 1 + 2. t + t 2 ∣ + c
∫ sec x d x = l n ∣ 1 2 − 2. t + t 2 1 2 + 2. t + t 2 ∣ + c
∫ sec x d x = l n ∣ ( 1 − t ) 2 ( 1 + t ) 2 ∣ + c
∫ sec x d x = l n ∣ ( 1 − t 1 + t ) 2 ∣ + c
∫ sec x d x = l n ∣ 1 − t 1 + t ∣ + c
∫ sec x d x = l n ∣ 1 − t an 2 x 1 + t an 2 x ∣ + c
∫ sec x d x = l n ∣ 1 − 1. t an 2 x 1 + t an 2 x ∣ + c
1 = t an 4 π
∫ sec x d x = l n ∣ 1 − t an 4 π . t an 2 x t an 4 π + t an 2 x ∣ + c
1 − t an p . t an q t an p + t an q = t an ( p + q )
∫ sec x d x = l n ∣ t an ( 4 π + 2 x ) ∣ + c