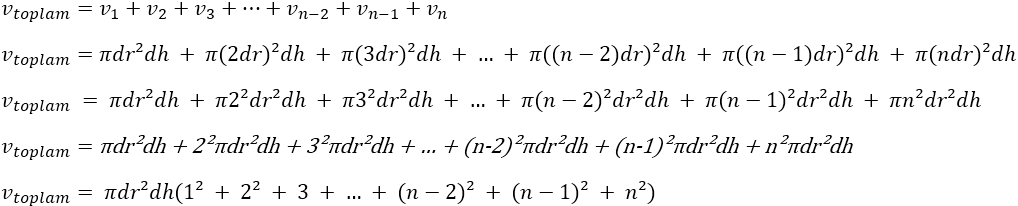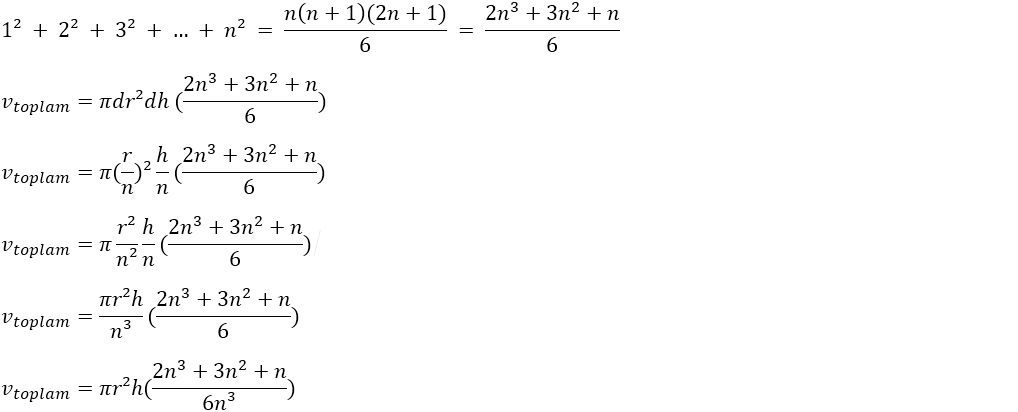Koninin Hacmi

Koni Nedir ? (Koninin Tanımı)

Bir dairenin her noktasını, dışındaki bir noktada birleştiren doğru parçalarının oluşturduğu geometrik şekle koni denir. Başka bir tanımı da, bir üçgenin herhangi bir kenarının etrafında 360 derece döndürülmesiyle elde edilen geometrik şekle denir. Dik (dönel) ve eğik koni olmak üzere ikiye ayrılır.

Koninin Hacim Formülü

Bir koninin hacmi her zaman için bir silindirin hacminin üçte birine (1/3'üne) eşittir.

Yukarıdaki şekildeki koninin hacmi;

Hacim = Taban Alanı x Yükseklik/3

V = π.r².h/3

Koninin Hacmi Nasıl Bulunur ?

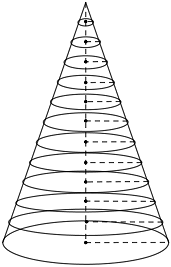
Koninin hacim formülü olan π.r².h/3'ün nereden geldiğini aşağıdaki şekildeki gibi ispatlayabiliriz.

Bir koninin hacmini doğrudan hesaplamak mümkün olmadığından ilk önce onu hacmini kolayca hesaplayabileceğimiz veya hacim formülünü bildiğimiz eşit yükseklikte sonsuz sayıda silindir şeklinde dilimlere ayırırız.

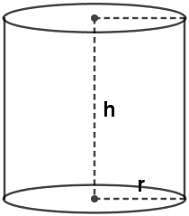
Yukarıdaki silindirin hacmi;

Hacim = Taban Alanı x Yükseklik

V = π.r².h

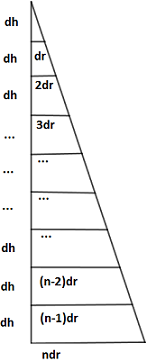
Konimizin yüksekliğine h dersek, sonsuz incelikteki her bir silindir diliminin yüksekliği h/n olur. dh = h/n'dir. Buradaki "n" sonsuz büyüklükte bir değeri ifade eder iken "dh" ise sonsuz küçüklükte bir değeri ifade eder. Aynı şekildeki dr = r/n'dir.

Şimdi en tepedeki silindirden başlamak üzere tüm silindirlerin hacimlerini sırasıyla toplayalım.

Örnek 1

Taban yarıçapının uzunluğu 4 cm ve yüksekliğinin uzunluğu 9 cm olan bir koninin hacminin değerini bulunuz ? (π = 3,14)

V = π.r².h/3

V = 3,14.(4 cm)².9 cm/3

V = 3,14.16 cm².9 cm/3

V = 452,16 cm³/3

V = 150,72 cm³

Örnek 2

Aynı yükseklikteki iki koninin hacimleri oranı 9/64'tir. Taban yarıçapları oranını bulunuz ?

1. kürenin hacmi v ve 2. kürenin hacmi V olsun.

v = π.r².h/3 = r².(π.h/3)

V = π.R².h/3 = R².(π.h/3)

π.h/3 = 1 olsun.

r² = 9

R² = 64 olur.

r²/R² = 9/64

(r/R)² = (3²/8²)

(r/R)² = (3/8)²

r/R = 3/8