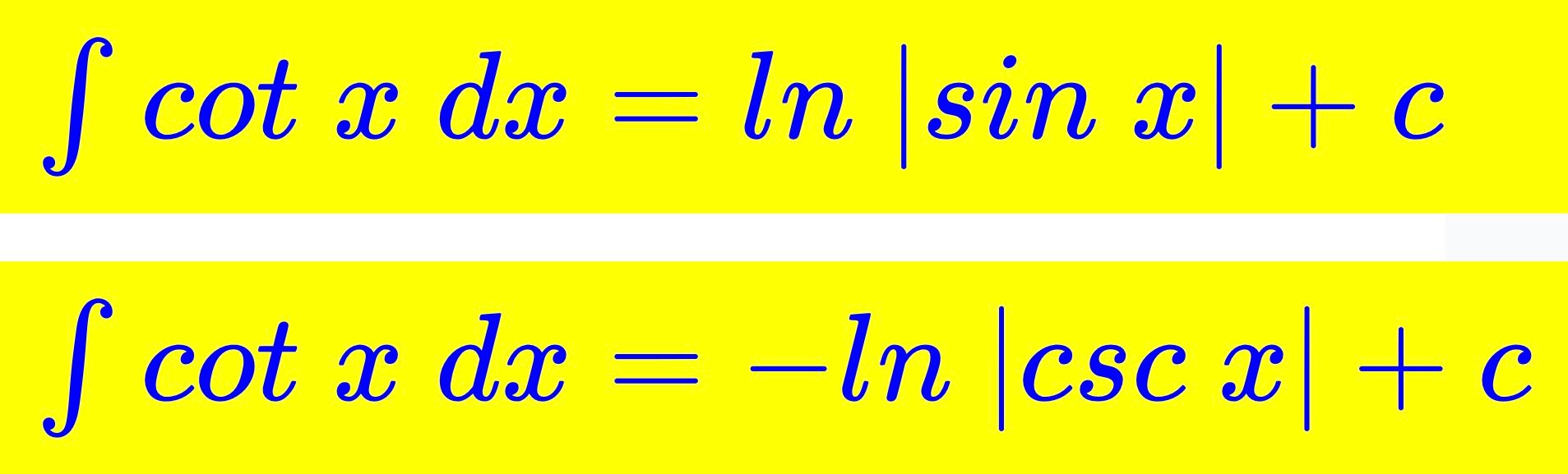Integral de Cot x

¿ Cuál es la Integral de Cot x ?

La integral de cot x es ln |sin x|+c.

$\int cotxdx=ln|sinx|+c$

$\int cotxdx=-ln|cscx|+c$

Encontrar la Integral de Cot x

Método 1

$\int cotxdx=?$

$cotx=\frac{cosx}{sinx}$

$\int cotxdx=\int \frac{cosx}{sinx}dx$

$\int cotxdx=\int \frac{cosxdx}{sinx}$

$sinx=u$

$d(sinx)=d(u)$

$d[f(x)]=f^{\prime }(x)dx$

$(sinx{)}^{\prime }dx=du$

$(sinx{)}^{\prime }=cosx$

$cosxdx=du$

$\int cotxdx=\int \frac{du}{u}$

$\int \frac{dx}{x}=ln|x|+c$

$\int cotxdx=ln|u|+c$

$\int cotxdx=ln|sinx|+c$

Método 2

$\int cotxdx=\int \frac{cscx.cotxdx}{cscx}$

$cscx=u$

$d(cscx)=d(u)$

$(cscx{)}^{\prime }dx=du$

$(cscx{)}^{\prime }=-cscx.cotx$

$-cscx.cotxdx=du$

$cscx.cotxdx=-du$

$\int cotxdx=\int \frac{-du}{u}$

$\int cotxdx=-\int \frac{du}{u}$

$\int cotxdx=-ln|u|+c$

$\int cotxdx=-ln|cscx|+c$

Método 3

$\int cotxdx=?$

$cotx=u$

$d(cotx)=d(u)$

$(cotx{)}^{\prime }dx=du$

$(cotx{)}^{\prime }=-(1+co{t}^{2}x)$

$-(1+co{t}^{2}x)dx=du$

$-(1+u^2)dx=du$

$dx=-\frac{du}{1+u^2}$

$\int cotxdx=\int u\frac{-du}{1+u^2}$

$\int cotxdx=\int \frac{-udu}{1+u^2}$

$1+u^2=v$

$d(1+u^2)=d(v)$

$(1+u^2{)}^{\prime }du=dv$

$\frac{\cancel{2}udu}{\cancel{2}}=\frac{dv}{2}$

$udu=\frac{dv}{2}$

$\int cotxdx=\int \frac{-\frac{dv}{2}}{v}$

$\int cotxdx=\int \frac{-\frac{1}{2}dv}{v}$

$\int cotxdx=-\frac{1}{2}\int \frac{dv}{v}$

$\int cotxdx=-\frac{1}{2}ln|v|+c$

$\int cotxdx=ln|v{|}^{-\frac{1}{2}}+c$

$\int cotxdx=ln|v^{-\frac{1}{2}}|+c$

$\int cotxdx=ln|\frac{1}{v^{\frac{1}{2}}}|+c$

$\int cotxdx=ln|\frac{1}{\sqrt{v}}|+c$

$\int cotxdx=ln|\frac{1}{\sqrt{1+u^2}}|+c$

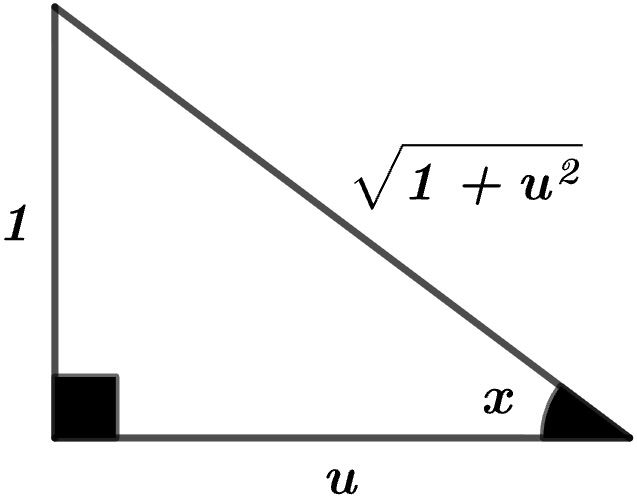
$cotx=u$

$sinx=\frac{1}{\sqrt{1+u^2}}$

$\int cotxdx=ln|sinx|+c$