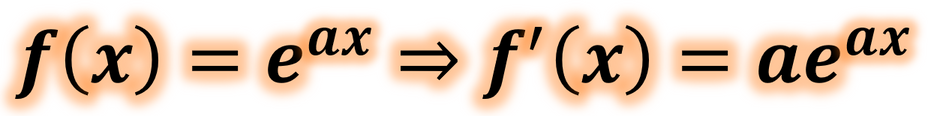f(x) = eᵃˣ ⇒ f'(x) = a.eᵃˣ'tir.
e üzeri ax'in türevi nedir ? f ( x ) = e a x ⇒ f ′ ( x ) = a . e a x olur.
e üzeri ax'in türevinin ispatı e a x 'in türevinin neden a . e a x 'e eşit olduğunu aşağıda bazılarını göstereceğimiz bir kaç yoldan ispatlayabiliriz.
1. Yol n → ∞ lim ( 1 + n 1 ) n = e = 2.71828...
n → ∞
n 1 → ∞ 1
n 1 → 0
h = n 1 dönüşümü yapılırsa;
h → 0
n → ∞ lim ( 1 + n 1 ) n = e
1/ n → 0 lim ( 1 + n 1 ) n = e
h → 0 lim ( 1 + h ) h 1 = e
h → 0 lim h 1 + h = e
f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x )
( e a x ) ′ = h → 0 lim h e a ( x + h ) − e a x
( e a x ) ′ = h → 0 lim h e a x + ah − e a x
( e a x ) ′ = h → 0 lim h e a x . ( e ah − 1 )
( e a x ) ′ = h → 0 lim e a x . h ( e ah − 1 )
( e a x ) ′ = e a x . h → 0 lim h ( e ah − 1 )
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim ( e ah − 1 )
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim e ah − h → 0 lim 1
( e a x ) ′ = e a x . h → 0 lim h ( h → 0 lim h 1 + h ) ah − h → 0 lim 1
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim ( h 1 + h ) ah − h → 0 lim 1
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim h ( 1 + h ) ah − h → 0 lim 1
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim h [( 1 + h ) a ] h − h → 0 lim 1
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim ( 1 + h ) a − h → 0 lim 1
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim [ ( 1 + h ) a − 1 ]
x n − 1 = ( x − 1 ) . ( x n − 1 + x n − 2 + x n − 3 + ... + x 3 + x 2 + x + 1 )
( e a x ) ′ = e a x . h → 0 lim h h → 0 lim ( 1 + h − 1 ) . [( 1 + h ) a − 1 + ( 1 + h ) a − 2 + ( 1 + h ) a − 3 + ... + 1 ]
( e a x ) ′ = e a x . h → 0 lim h h . [( 1 + h ) a − 1 + ( 1 + h ) a − 2 + ( 1 + h ) a − 3 + ... + 1 )]
( e a x ) ′ = e a x . [( 1 + 0 ) a − 1 + ( 1 + 0 ) a − 2 + ( 1 + 0 ) a − 3 + ... + 1 ]
( e a x ) ′ = e a x . ( 1 a − 1 + 1 a − 2 + 1 a − 3 + ... + 1 )
( e a x ) ′ = e a x . a tane ( 1 + 1 + 1 + ... + 1 )
( e a x ) ′ = a . e a x
2. Yol f ( x ) = e a x
l n f ( x ) = l n e a x
l n f ( x ) = a x . l n e
l n f ( x ) = a x .1
l n f ( x ) = a x
[ l n f ( x ) ] ′ = ( a x ) ′
f ( x ) = l n g ( x ) ⇒ f ′ ( x ) = g ( x ) g ′ ( x )
f ( x ) f ′ ( x ) = a
f ′ ( x ) = a . f ( x )
f ′ ( x ) = a . e a x
3. Yol e a x fonksiyonunun sonsuz seri şeklindeki açılımından faydalanarak da e a x 'in türevinin a . e a x 'e eşit olduğunu ispatlayabiliriz. e a x fonksiyonunun soru seri şeklindeki açılımı aşağıdaki gibidir.
e a x = 1 + a . x + 2 ! ( a . x ) 2 + 3 ! ( a . x ) 3 + 4 ! ( a . x ) 4 + 5 ! ( a . x ) 5 + ...
e a x = 1 + a . x + 2 ! a 2 . x 2 + 3 ! a 3 . x 3 + 4 ! a 4 . x 4 + 5 ! a 5 . x 5 + ...
( e a x ) ′ = ( 1 + a . x + 2 ! a 2 . x 2 + 3 ! a 3 . x 3 + 4 ! a 4 . x 4 + 5 ! a 5 . x 5 + ... ) ′ (eşitliğin her iki tarafının da türevini alırız)
( e a x ) ′ = ( 1 ) ′ + ( a . x ) ′ + ( 2 ! a 2 . x 2 ) ′ + ( 3 ! a 3 . x 3 ) ′ + ( 4 ! a 4 . x 4 ) ′ + ( 5 ! a 5 . x 5 ) ′ + ...
( e a x ) ′ = 0 + a + 2 .1 ! 2 . a 2 . x + 3 .2 ! 3 . a 3 . x 2 + 4 .3 ! 4 . a 4 . x 3 + 5 .4 ! 5 . a 5 . x 4 + ...
( e a x ) ′ = a + a 2 . x + 2 ! a 3 . x 2 + 3 ! a 4 . x 3 + 4 ! a 5 . x 4 + ...
( e a x ) ′ = a . ( 1 + a . x + 2 ! a 2 . x 2 + 3 ! a 3 . x 3 + 4 ! a 4 . x 4 + ... )
( e a x ) ′ = a . ( 1 + a . x + 2 ! ( a . x ) 2 + 3 ! ( a . x ) 3 + 4 ! ( a . x ) 4 + ... )
( e a x ) ′ = a . e a x