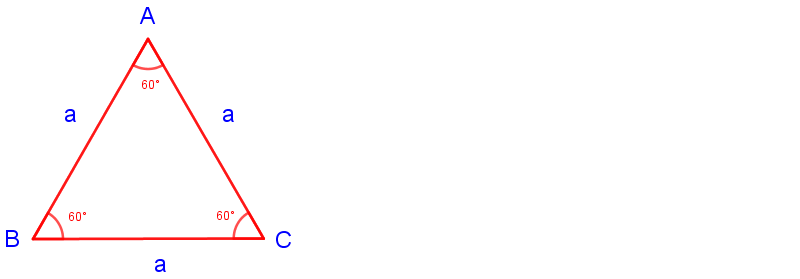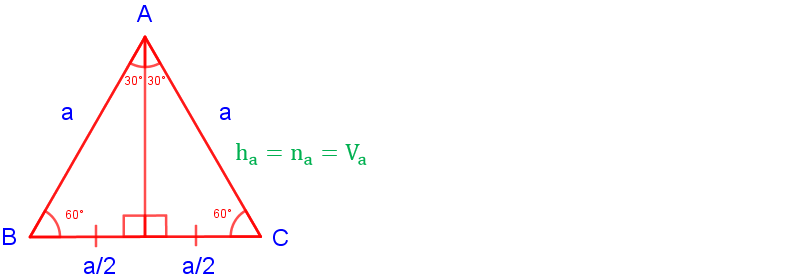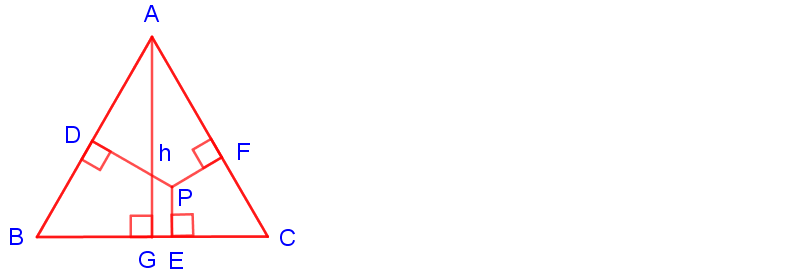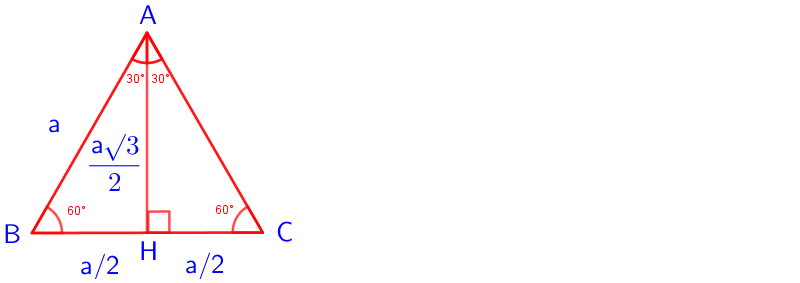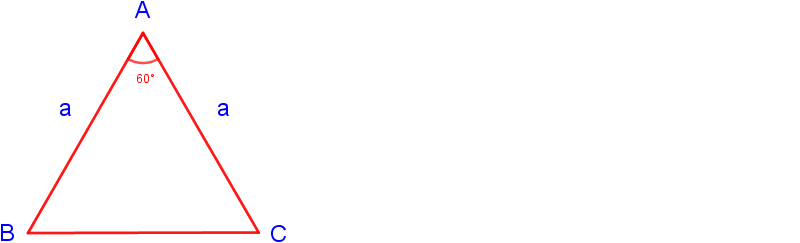Eşkenar Üçgen

Eşkenar Üçgen Nedir?

Üç kenarının uzunluğu da birbirine eşit olan üçgenlere eşkenar üçgen denir.

Yukarıdaki şekildeki ABC üçgeni bir eşkenar üçgen olup;

1. |AB| = |AC| = |BC| = a

2. m(A) = m(B) = m(C) = 60°'dir.

Eşkenar Üçgen Özellikleri

1. Bir eşkenar üçgende bütün kenar uzunlukları birbirine eşittir.

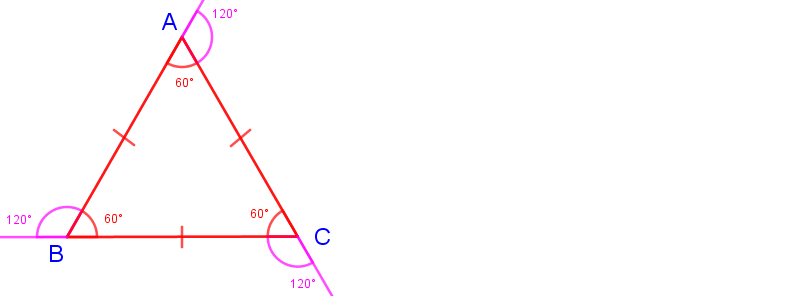
2. Bir eşkenar üçgende bütün iç açıların ölçüleri birbirine eşit ve 60° ve bütün dış açıların ölçüleri birbirine eşit ve 120°'dir.

3. Bir eşkenar üçgende yükseklik (h), açıortay (n) ve kenarortay (V) aynıdır.

4. Bir eşkenar üçgenin üzerinden veya içinden alınan herhangi bir noktadan kenarlara inilen dikmelerin toplam uzunluğu, eşkenar üçgenin yüksekliği kadardır.

Yukarıdaki şekildeki ABC üçgeni bir eşkenar üçgen olmak üzere;

|PD| + |PE| + |PF| = |AG| = h

5. Eşkenar üçgenin içerisinden alınan herhangi bir noktadan kenarlarına çizilen paralellerin toplam uzunluğu, eşkenar üçgenin bir kenarının uzunluğu kadardır.

Yukarıdaki şekildeki ABC üçgeni bir eşkenar üçgen ve [AB] // [FP], [BC] // [DP] ve [CA] // [EP] olmak üzere;

|DP| + |EP| + |FP| = a

Eşkenar Üçgen Alanı (Eşkenar Üçgenin Alanı)

Eşkenar Üçgenin Alanı Nasıl Bulunur?

1. Yol

Yukarıdaki şekildeki ABC eşkenar üçgenin alanı, taban kenarı ile yüksekliğinin çarpımına eşittir.

A (ABC) = |BC| . |AH| / 2

AHB veya AHC dik üçgenlerinden herhangi birine Pisagor Teoremi'ni uygularsak;

|AH|² + |BH|² = |AB|²

|AH| = h

h² + (a/2)² = a²

h² + a²/4 = a²

h² = a² - a²/4

h² = 3a²/4

√h² = √3a²/4

h = a√3/2

|AH| = a√3/2

A(ABC) = |BC| . |AH| / 2

A(ABC) = a . a√3/2 / 2 = a²√3/4 olur.

2. Yol

Sinüs Teoremi'ne göre iki kenarı ve bu iki kenarı arasındaki açının ölçüsü bilinen bir ABC üçgeninin alanı;

A (ABC) = 1/2 . b . c . sinA'dır.

A (ABC) = 1/2 . a . a . sin60

sin60 = √3/2

A (ABC) = 1/2 . a . a . √3/2

A (ABC) = a²√3/4 olur.

3. Yol

Heron Formülü'ne göre üç kenarının uzunluğu da bilinen herhangi bir ABC üçgenin alanı, s = (a + b + c)/2 olmak üzere;

A(ABC) = √s . √s - a . √s - b . √s - c

s = (a + a + a)/2 = 3a/2

A(ABC) = √3a/2 . √3a/2 - a . √3a/2 - a . √3a/2 - a

A(ABC) = √3a/2 . √a/2 . √a/2 . √a/2

A(ABC) = √3a⁴/16

A(ABC) = a²√3/4 olur.