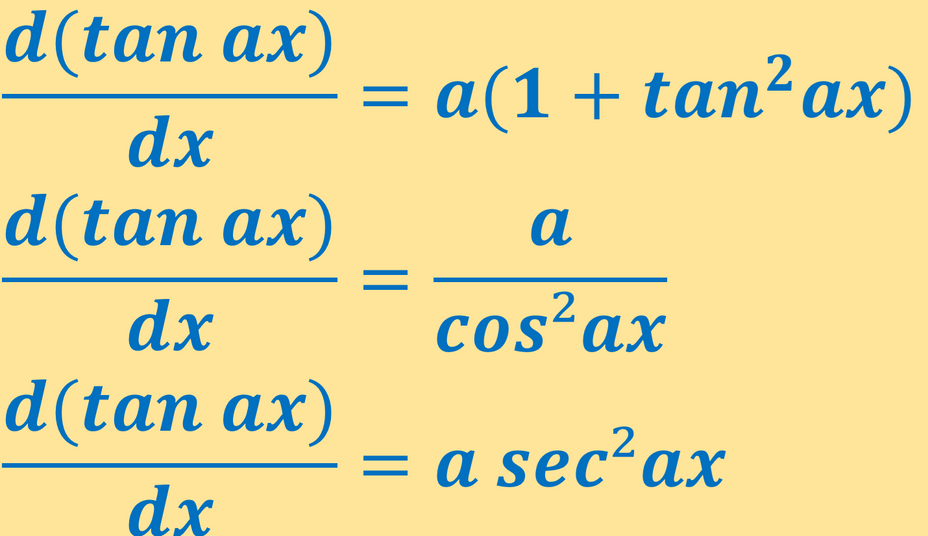The derivative of tan ax is a.(1+tan² ax).
What is the Derivative of Tan ax ? The derivative of tan ax is a.(1+tan² ax).
( t an a x ) ′ = a . ( 1 + t a n 2 a x )
d x d ( t an a x ) = a . ( 1 + t a n 2 a x )
Proof of the Derivative of Tan ax Way 1 f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) ( t an a x ) ′ = h → 0 lim h t an a ( x + h ) − t an a x ( t an a x ) ′ = h → 0 lim h t an ( a x + ah ) − t an a x t an ( p + q ) = 1 − t an p . t an q t an p + t an q ( t an a x ) ′ = h → 0 lim h 1 − t an a x . t an ah t an a x + t an ah − t an a x ( t an a x ) ′ = h → 0 lim h 1 − t an a x . t an ah t an a x + t an ah − t an a x . ( 1 − t an a x . t an ah ) ( t an a x ) ′ = h → 0 lim h 1 − t an a x . t an ah t an a x + t an ah − t an a x + t a n 2 a x . t an ah ( t an a x ) ′ = h → 0 lim h 1 − t an a x . t an ah t an ah + t a n 2 a x . t an ah ( t an a x ) ′ = h → 0 lim h 1 − t an a x . t an ah t an ah . ( 1 + t a n 2 a x ) ( t an a x ) ′ = h → 0 lim [ h 1 . 1 − t an a x . t an ah t an ah . ( 1 + t a n 2 a x ) ] ( t an a x ) ′ = h → 0 lim h . ( 1 − t an a x . t an ah ) t an ah . ( 1 + t a n 2 a x ) ( t an a x ) ′ = h → 0 lim a . h . ( 1 − t an a x . t an ah ) a . t an ah . ( 1 + t a n 2 a x ) ( t an a x ) ′ = a . h → 0 lim ah . ( 1 − t an a x . t an ah ) t an ah . ( 1 + t a n 2 a x ) ( t an a x ) ′ = a . h → 0 lim ( ah t an ah . 1 − t an a x . t an ah 1 + t a n 2 a x ) ( t an a x ) ′ = a . h → 0 lim ah t an ah . h → 0 lim 1 − t an a x . t an ah 1 + t a n 2 a x h → 0 ( ah = h )
( t an a x ) ′ = a . h → 0 lim h t an h . h → 0 lim 1 − t an a x . t an h 1 + t a n 2 a x
t → 0 l i m t t an t = 1
( t an a x ) ′ = a .1. 1 − t an a x . t an 0 1 + t a n 2 a x
t an 0 = 0
( t an a x ) ′ = a .1. 1 − t an a x .0 1 + t a n 2 a x
( t an a x ) ′ = a .1. 1 − 0 1 + t a n 2 a x
( t an a x ) ′ = a .1. 1 1 + t a n 2 a x
( t an a x ) ′ = a .1. ( 1 + t a n 2 a x )
( t an a x ) ′ = a . ( 1 + t a n 2 a x )
Way 2 f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) ( t an a x ) ′ = h → 0 lim h t an a ( x + h ) − t an a x
( t an a x ) ′ = h → 0 lim h t an ( a x + ah ) − t an a x
t an x = cos x s in x
( t an a x ) ′ = h → 0 lim h cos ( a x + ah ) s in ( a x + ah ) − cos a x s in a x
( t an a x ) ′ = h → 0 lim h cos a x . cos ( a x + ah ) s in ( a x + ah ) . cos a x − cos ( a x + ah ) . s in a x
s in p . cos q − cos p . s in q = s in ( p − q )
( t an a x ) ′ = h → 0 lim h cos a x . cos ( a x + ah ) s in ( a x + ah − a x )
( t an a x ) ′ = h → 0 lim h cos a x . cos ( a x + ah ) s in ah
( t an a x ) ′ = h → 0 lim [ h 1 . cos a x . cos ( a x + ah ) s in ah ]
( t an a x ) ′ = h → 0 lim h . cos a x . cos ( a x + ah ) s in ah
( t an a x ) ′ = h → 0 lim a . h . cos a x . cos ( a x + ah ) a . s in ah
( t an a x ) ′ = a . h → 0 lim ah . cos a x . cos ( a x + ah ) s in ah
( t an a x ) ′ = a . h → 0 lim [ ah s in ah . cos a x . cos ( a x + ah ) 1 ]
( t an a x ) ′ = a . h → 0 lim ah s in ah . h → 0 lim cos a x . cos ( a x + ah ) 1
h → 0 ( ah = h )
( t an a x ) ′ = a . h → 0 lim h s in h . h → 0 lim cos a x . cos ( a x + h ) 1
t → 0 l i m t s in t = 1
( t an a x ) ′ = a .1. cos a x . cos ( a x + 0 ) 1
( t an a x ) ′ = a .1. cos a x . cos a x 1
( t an a x ) ′ = co s 2 a x a .1.1
( t an a x ) ′ = co s 2 a x a
( t an a x ) ′ = a . co s 2 a x 1
( t an a x ) ′ = a . ( cos a x 1 ) 2
cos x 1 = sec x
( t an a x ) ′ = a . se c 2 a x
( t an a x ) ′ = a . ( 1 + t a n 2 a x ) = co s 2 a x a = a . se c 2 a x