Derivative of Arcsin x

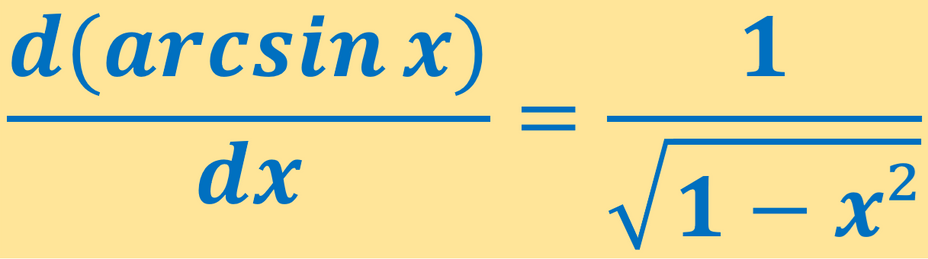
What is the Derivative of Arcsin x ?

The derivative of arcsin x is 1/√1-x².

$(arcsinx{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}$

$\frac{d}{dx}(arcsinx)=\frac{1}{\sqrt{1-x^2}}$

Proof of the Derivative of Arcsin x

Way 1

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

$(arcsinx{)}^{\prime }=\underset{h\to 0}{\lim }\frac{arcsin(x+h)-arcsinx}{h}$

$arcsin(x+h)=U$, $sinU=x+h$

$arcsinx=V$, $sinV=x$

$sinU-sinV=\cancel{x}+h-\cancel{x}$

$sinU-sinV=h$

$h\to 0$, $sinU-sinV\to 0$, $sinU\to sinV$, $U\to V$

$(arcsinx{)}^{\prime }=\underset{U\to V}{\lim }\frac{U-V}{sinU-sinV}$

$\boxed{sinp-sinq=2.sin\frac{p-q}{2}.cos\frac{p+q}{2}}$

$(arcsinx{)}^{\prime }=\underset{U\to V}{\lim }\frac{U-V}{2.sin\frac{U-V}{2}.cos\frac{U+V}{2}}$

$(arcsinx{)}^{\prime }=\underset{U\to V}{\lim }\frac{\frac{1}{2}.(U-V)}{sin\frac{U-V}{2}.cos\frac{U+V}{2}}$

$(arcsinx{)}^{\prime }=\underset{U\to V}{\lim }\frac{\frac{U-V}{2}}{sin\frac{U-V}{2}.cos\frac{U+V}{2}}$

$(arcsinx{)}^{\prime }=\underset{U\to V}{\lim }(\frac{\frac{U-V}{2}}{sin\frac{U-V}{2}}.\frac{1}{cos\frac{U+V}{2}})$

$(arcsinx{)}^{\prime }=\underset{U\to V}{\lim }\frac{\frac{U-V}{2}}{sin\frac{U-V}{2}}.\underset{U\to V}{\lim }\frac{1}{cos\frac{U+V}{2}}$

$U\to V$, $\frac{U-V}{2}\to 0$

$(arcsinx{)}^{\prime }=\underset{\frac{U-V}{2}\to 0}{\lim }\frac{\frac{U-V}{2}}{sin\frac{U-V}{2}}.\underset{U\to V}{\lim }\frac{1}{cos\frac{U+V}{2}}$

$\boxed{\underset{t\to 0}{\lim }\frac{t}{sint}=1}$

$(arcsinx{)}^{\prime }=1.\frac{1}{cos\frac{V+V}{2}}$

$(arcsinx{)}^{\prime }=\frac{1}{cos\frac{V+V}{2}}$

$(arcsinx{)}^{\prime }=\frac{1}{cos\frac{\cancel{2}V}{\cancel{2}}}$

$(arcsinx{)}^{\prime }=\frac{1}{cosV}$

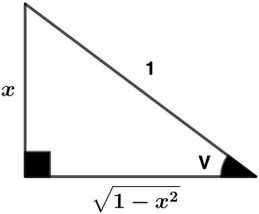
$sinV=x$

$cosV=\sqrt{1-x^2}$

$(arcsinx{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}$

Way 2

$y=arcsinx$

$siny=x$

$(siny{)}^{\prime }=(x{)}^{\prime }$

$\boxed{(sinu{)}^{\prime }=u^{\prime }.cosu}$

$y^{\prime }.cosy=1$

$y^{\prime }=\frac{1}{cosy}$

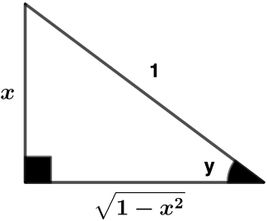
$siny=x$

$cosy=\sqrt{1-x^2}$

$y^{\prime }=\frac{1}{\sqrt{1-x^2}}$