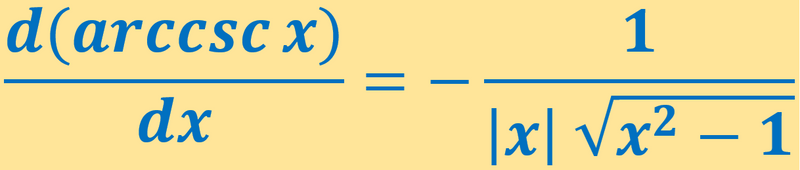La derivada de arccsc x es -1/(|x|.√x²-1).
¿ Cuál es la Derivada de Arccsc x ? La derivada de arccsc x es -1/(|x|.√x²-1).
( a rccsc x ) ′ = − ∣ x ∣. x 2 − 1 1
d x d ( a rccsc x ) = − ∣ x ∣. x 2 − 1 1
Prueba de la Derivada de Arccsc x Método 1 f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x )
( a rccsc x ) ′ = h → 0 lim h a rccsc ( x + h ) − a rccsc x
a rccsc ( x + h ) = U , csc U = x + h a rccsc x = V , csc V = x csc U − csc V = x + h − x csc U − csc V = h h → 0 , csc U − csc V → 0 , csc U → csc V , U → V ( a rccsc x ) ′ = U → V lim csc U − csc V U − V csc a − csc b = s in a . s in b s in b − s in a ( a rccsc x ) ′ = U → V lim s in U . s in V s in V − s in U U − V ( a rccsc x ) ′ = U → V lim s in V − s in U ( U − V ) . s in U . s in V s in p − s in q = 2. cos 2 p + q . s in 2 p − q ( a rccsc x ) ′ = U → V lim 2. cos 2 V + U . s in 2 V − U ( U − V ) . s in U . s in V ( a rccsc x ) ′ = U → V lim 2. cos 2 V + U . s in 2 V − U − ( V − U ) . s in U . s in V ( a rccsc x ) ′ = − U → V lim 2. cos 2 V + U . s in 2 V − U ( V − U ) . s in U . s in V ( a rccsc x ) ′ = − U → V lim cos 2 V + U . s in 2 V − U 2 1 . ( V − U ) . s in U . s in V ( a rccsc x ) ′ = − U → V lim cos 2 V + U . s in 2 V − U 2 V − U . s in U . s in V ( a rccsc x ) ′ = − U → V lim ( s in 2 V − U 2 V − U . cos 2 V + U s in U . s in V ) ( a rccsc x ) ′ = − U → V lim s in 2 V − U 2 V − U . U → V lim cos 2 V + U s in U . s in V U → V , V → U , 2 V − U → 0 ( a rccsc x ) ′ = − 2 V − U → 0 lim s in 2 V − U 2 V − U . U → V lim cos 2 V + U s in U . s in V t → 0 l i m s in t t = 1 ( a rccsc x ) ′ = − 1. cos 2 V + V s in V . s in V
( a rccsc x ) ′ = − cos 2 V + V s in V . s in V
( a rccsc x ) ′ = − cos 2 2 V s i n 2 V
( a rccsc x ) ′ = − cos V s i n 2 V
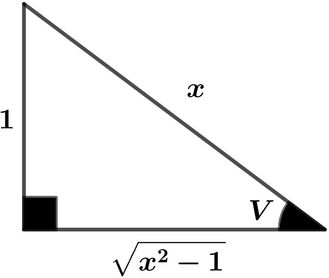
csc V = x
s in V = x 1
cos V = x x 2 − 1
( a rccsc x ) ′ = − x x 2 − 1 ( x 1 ) 2
( a rccsc x ) ′ = − x x 2 − 1 x 2 1
( a rccsc x ) ′ = − x 2 x 1 . x 2 − 1 x 1
( a rccsc x ) ′ = − x . x 2 − 1 1
Como la pendiente de la tangente en cualquier punto de la función arcccsc x siempre será menor que 0, naturalmente el valor de su derivada en cualquier punto también será menor que 0. Para esto, necesitamos mostrar la x en el denominador en la fórmula anterior en valor absoluto.
( a rccsc x ) ′ = − ∣ x ∣. x 2 − 1 1
Método 1 y = a rccsc x
csc y = x
( csc y ) ′ = ( x ) ′
( csc u ) ′ = − u ′ . csc u . co t u
− y ′ . csc y . co t y = 1
y ′ = − csc y . co t y 1
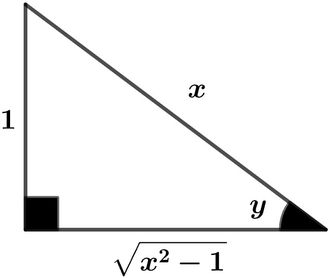
csc y = x
co t y = x 2 − 1
y ′ = − x . x 2 − 1 1
y ′ = − ∣ x ∣. x 2 − 1 1