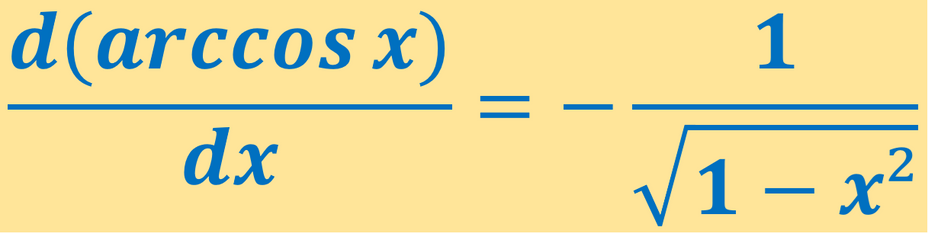La derivada de arccos x es -1/√1-x².
¿ Cuál es la Derivada de Arccos x ? La derivada de arccos x es -1/√1-x².
( a rccos x ) ′ = − 1 − x 2 1
d x d ( a rccos x ) = − 1 − x 2 1
Prueba de la Derivada de Arccos x Método 1 f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x )
( a rccos x ) ′ = h → 0 lim h a rccos ( x + h ) − a rccos x
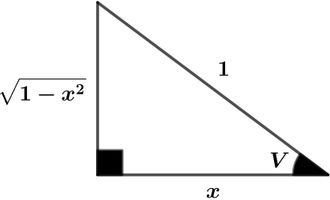
a rccos ( x + h ) = U , cos U = x + h a rccos x = V , cos V = x cos U − cos V = x + h − x cos U − cos V = h h → 0 , cos U − cos V → 0 , cos U → cos V , U → V ( a rccos x ) ′ = U → V lim cos U − cos V U − V cos p − cos q = − 2. s in 2 p + q . s in 2 p − q ( a rccos x ) ′ = U → V lim − 2. s in 2 U + V . s in 2 U − V U − V ( a rccos x ) ′ = U → V lim s in 2 U + V . s in 2 U − V − 2 1 . ( U − V ) ( a rccos x ) ′ = U → V lim s in 2 U + V . s in 2 U − V − 2 U − V ( a rccos x ) ′ = − U → V lim s in 2 U + V . s in 2 U − V 2 U − V ( a rccos x ) ′ = − U → V lim ( s in 2 U − V 2 U − V . s in 2 U + V 1 ) ( a rccos x ) ′ = − U → V lim s in 2 U − V 2 U − V . U → V lim s in 2 U + V 1 U → V , 2 U − V → 0 ( a rccos x ) ′ = − 2 U − V → 0 lim s in 2 U − V 2 U − V . U → V lim s in 2 U + V 1 t → 0 l i m s in t t = 1
( a rccos x ) ′ = − 1. s in 2 V + V 1
( a rccos x ) ′ = − s in 2 V + V 1
( a rccos x ) ′ = − s in 2 2 V 1
( a rccos x ) ′ = − s in V 1
cos V = x
s in V = 1 − x 2
( a rccos x ) ′ = − 1 − x 2 1
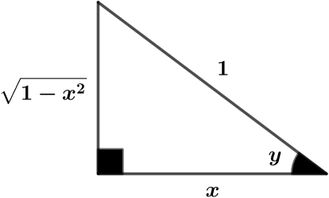
Método 2 y = a rccos x
cos y = x
( cos y ) ′ = ( x ) ′
( cos u ) ′ = − u ′ . s in u
− y ′ . s in y = 1
y ′ = − s in y 1
cos y = x
s in y = 1 − x 2
y ′ = − 1 − x 2 1