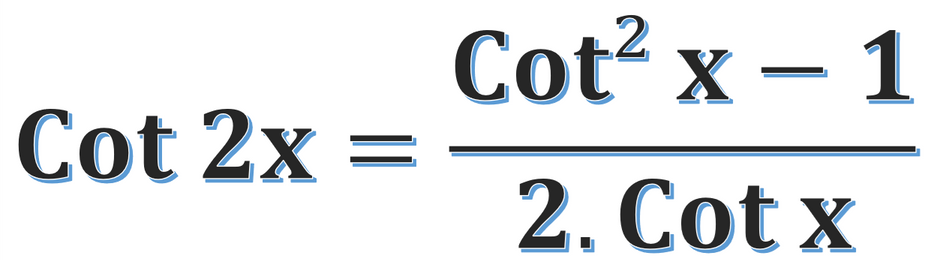Cot 2x Formula

Pow
August 09, 2024
Cot 2x = (Cot² x - 1)/2.Cot x
What is the formula for Cot 2x ?
Cot 2x is equal to (Cot² x - 1)/2.Cot x.
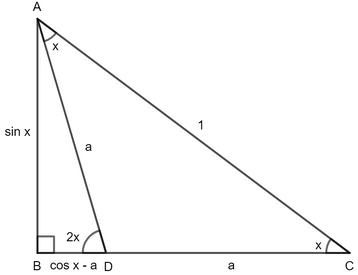
Proof of Cot 2x's Formula
In the right triangle ABC above;
'dır.
For triangle ABC;
For triangle ABD;
In the ABD triangle;
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.