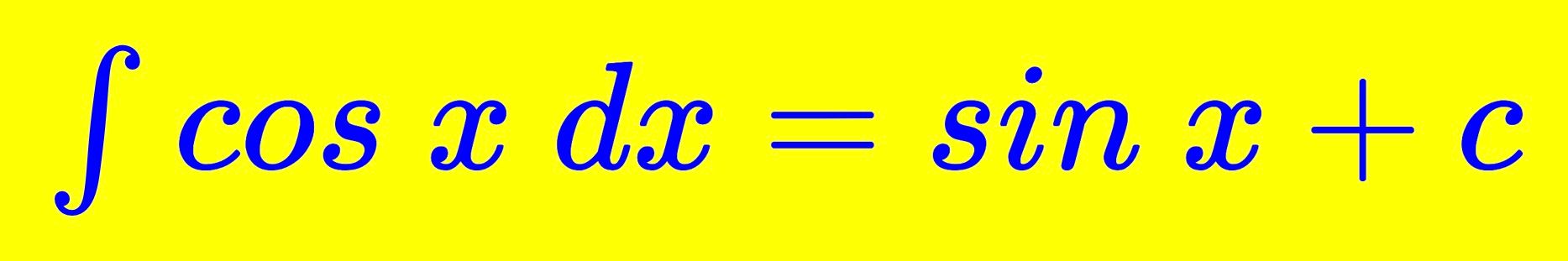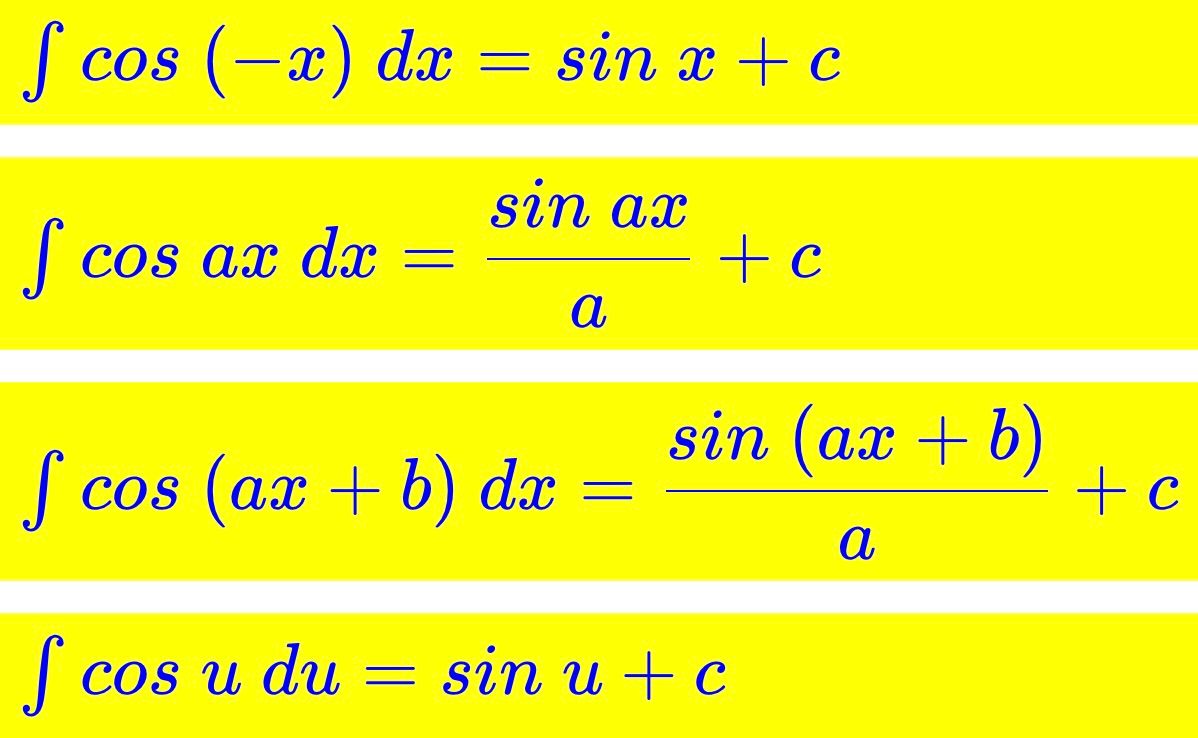Cos x'in İntegrali

Pow
August 16, 2025
Cos x'in integrali sin x+c'dir.
Cos x'in İntegrali Nedir ?
Cos x'in integrali sin x+c'dir.
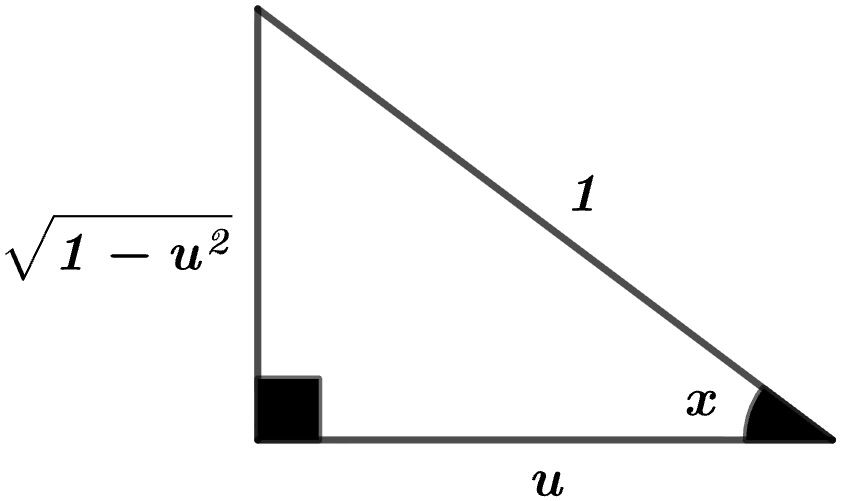
Cos x'in İntegralini Bulma
Önemli Formüller
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.