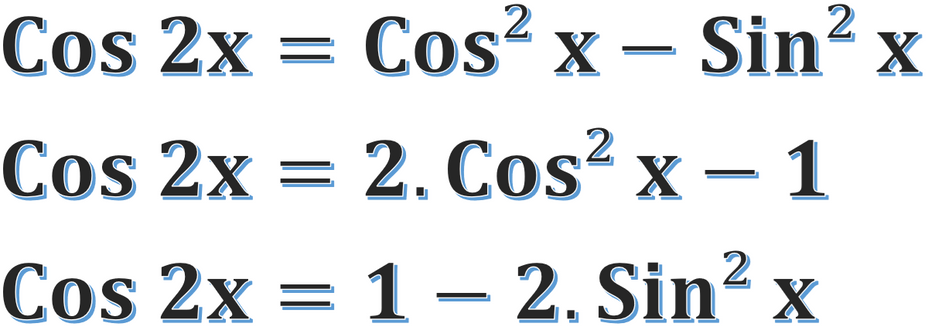Cos 2x Formula

What is the formula for Cos 2x ?

Cos 2x are equal to cos² x - sin² x, 2.cos² x - 1 or 1 - 2.sin² x.

Proof of Cos 2x's Formula

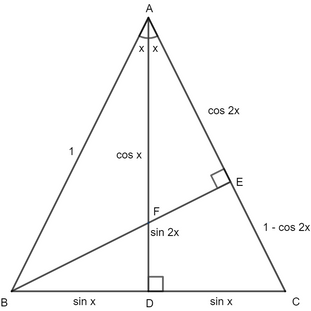
Way 1

In the above isosceles triangle ABC;

$AB=AC=1$

$BD=DC=\sin x$

$AD=\cos x$

$BE=\sin 2x$

$AE=\cos 2x$

$EC=1-\cos 2x$.

For right triangle BEC;

$(\sin 2x{)}^2+(1-\cos 2x{)}^2=(2.\sin x{)}^2$

${\sin }^{2}2x+1^2-\mathrm{2.1.}\cos 2x+{\cos }^{2}2x=4.{\sin }^{2}x$

${\sin }^{2}2x+1-2.\cos 2x+{\cos }^{2}2x=4.{\sin }^{2}x$

${\sin }^{2}2x+{\cos }^{2}2x+1-2.\cos 2x=4.{\sin }^{2}x$

$\boxed{{\sin }^{2}x+{\cos }^{2}x=1}$

$1+1-2.\cos 2x=4.{\sin }^{2}x$

$2-2.\cos 2x=4.{\sin }^{2}x$

$2.(1-\cos 2x)=4.{\sin }^{2}x$

$1-\cos 2x=2.{\sin }^{2}x$

$-\cos 2x=2.{\sin }^{2}x-1$

$\underline{\cos 2x=1-2.{\sin }^{2}x}$

$\cos 2x={\sin }^{2}x+{\cos }^{2}x-2.{\sin }^{2}x$

$\cos 2x={\cos }^{2}x+{\sin }^{2}x-2.{\sin }^{2}x$

$\underline{\cos 2x={\cos }^{2}x-{\sin }^{2}x}$

$\boxed{{\sin }^{2}x=1-{\cos }^{2}x}$

$\cos 2x={\cos }^{2}x-(1-{\cos }^{2}x)$

$\cos 2x={\cos }^{2}x-1+{\cos }^{2}x$

$\cos 2x={\cos }^{2}x+{\cos }^{2}x-1$

$\underline{\cos 2x=2.{\cos }^{2}x-1}$

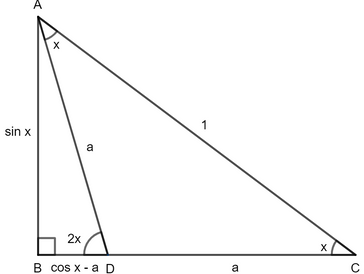
Way 2

In the right triangle ABC above;

$AC=1$

$AB=\sin x$

$BC=\cos x$

$AD=DC=a$

$BD=\cos x-a$'dır.

For triangle ABC;

$(AB{)}^2+(BC{)}^2=(AC{)}^2$

${\sin }^{2}x+{\cos }^{2}x=1^2$

${\sin }^{2}x+{\cos }^{2}x=1$

For triangle ABD;

$(AB{)}^2+(BD{)}^2=(AD{)}^2$

${\sin }^{2}x+(\cos x-a{)}^2=a^2$

${\sin }^{2}x+{\cos }^{2}x-2.\cos x.a+a^2=a^2$

${\sin }^{2}x+{\cos }^{2}x-2.\cos x.a+\cancel{a^2}-\cancel{a^2}=0$

$1-2.\cos x.a=0$

$-2.\cos x.a=-1$

$\frac{\cancel{-2.\cos x}.a}{\cancel{-2.\cos x}}=\frac{-1}{-2.\cos x}$

$a=\frac{1}{2.\cos x}$

In triangle ABC;

$\cos 2x=\frac{BD}{AD}=\frac{\cos x-a}{a}$

$\cos 2x=\frac{\cos x-\frac{1}{2.\cos x}}{\frac{1}{2.\cos x}}$

$\cos 2x=\frac{\frac{2.\cos x.\cos x-1}{2.\cos x}}{\frac{1}{2.\cos x}}$

$\cos 2x=\frac{\frac{2.{\cos }^{2}x-1}{\cancel{2.\cos x}}}{\frac{1}{\cancel{2.\cos x}}}$

$\underline{\cos 2x=2.{\cos }^{2}x-1}$

$\boxed{{\cos }^{2}x=1-{\sin }^{2}x}$

$\cos 2x=2.(1-{\sin }^{2}x)-1$

$\cos 2x=2-2.{\sin }^{2}x-1$

$\cos 2x=2-1-2.{\sin }^{2}x$

$\underline{\cos 2x=1-2.{\sin }^{2}x}$

$\cos 2x={\sin }^{2}x+{\cos }^{2}x-2.{\sin }^{2}x$

$\cos 2x={\cos }^{2}x+{\sin }^{2}x-2.{\sin }^{2}x$

$\underline{\cos 2x={\cos }^{2}x-{\sin }^{2}x}$

Way 3

Formulas used to find the trigonometric value of the sum or difference of two angles with known trigonometric values ​​are called sum-difference formulas. We can find the value of the formula for cos 2x by using the following sum formula for cosine.

$\boxed{\cos (a+b)=\cos a.\cos b-\sin a.\sin b}$

$\cos 2x=\cos (x+x)$

$\cos 2x=\cos x.\cos x-\sin x.\sin x$

$\cos 2x={\cos }^{2}x-{\sin }^{2}x$