Bağımlı ve Bağımsız Değişkenler
Bir deney sırasında bağımsız ve bağımlı değişken değerlerinin hassas bir şekilde ölçülerek kaydedilmesi kritik bir öneme sahiptir. Bir matematiksel denklem de

Pow
@powBir matematiksel denklem de veya deneyde değerini istediğimiz şekilde değiştirebildiğimiz (oynayabildiğimiz) değişkene bağımsız değişken denir.
Bir matematiksel denklem de veya deneyde değeri bağımsız değişkenin değerindeki değişime bağlı olarak değişen ve istediğimiz şekilde değiştiremediğimiz (oynayamadığımız) değişkene ise bağımlı değişken denir.
Bağımsız değişkenin değerini istediğimiz şekilde değiştirebiliriz ama bağımlı değişkenin değerindeki değişim bizim kontrolümüzde değildir.
Bağımsız - Bağımlı Değişkenlere Günlük Hayattan Örnekler
Bir cismin hareketinden kaynaklanan kinetik enerjisi (Ek = 1/2.m.v²) o cismin hızının karesiyle doğru orantılıdır. Burada cismin hızı bağımsız değişken iken kinetik enerjisi bağımlı değişkendir.
Bir cismin sıcaklığı onu oluşturan taneciklerin ortalama kinetik enerjileri ile doğru orantılıdır. Burada taneciklerin ortalama kinetik enerjisi bağımsız değişken iken cismin sıcaklığı bağımlı değişkendir.
Bir devredeki elektrik akımının şiddeti devreden geçen elektron sayısı ile doğru orantılıdır. Burada elektron sayısı bağımsız değişken iken akım şiddeti bağımlı değişkendir.
Bir aracın tükettiği benzin miktarı aldığı yol ile doğru orantılıdır. Burada tüketilen benzin miktarı bağımsız değişken iken alınan yol bağımlı değişkendir.
Sabit bir yüzeye uygulanan kuvvet ile basınç miktarı doğru orantılıdır. Burada uygulanan kuvvet bağımsız değişken iken basınç miktarı bağımlı değişkendir.
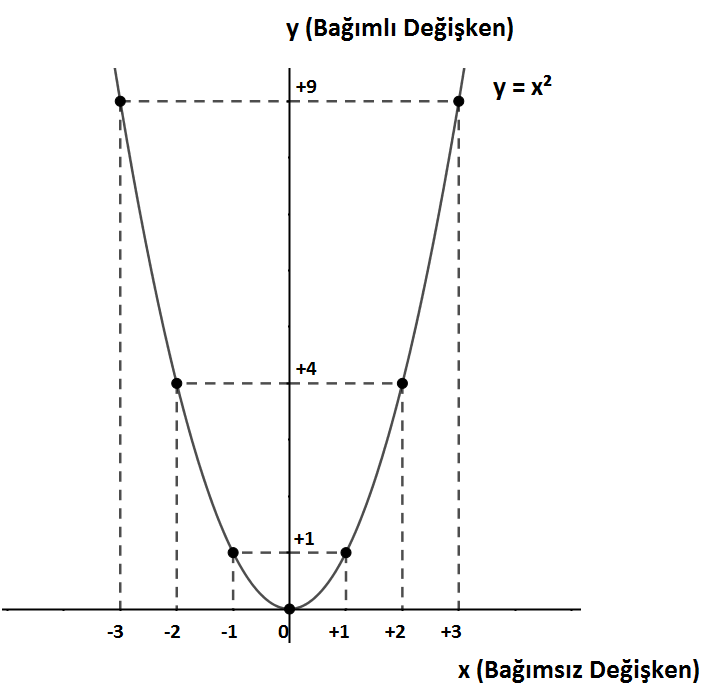
Yukarıdaki tabloda da görüleceği üzere y = x² denkleminde x bağımsız bir değiş iken y, x’e bağlı bağımlı bir değişkendir.
Yukarıdaki y = x² denkleminin grafiğinden de anlaşılacağı üzere x bağımsız değişkenindeki herhangi bir değişim y bağımlı değişkenine de hemen yansımakta ve onun değerinde de bir değişime neden olmaktadır.
Belirli bir yükseklikten serbest düşmeye bırakılan bir cismin hareketini inceleyerek bağımsız ve bağımlı değişkenin ne olduğunu açıklamaya çalışalım.
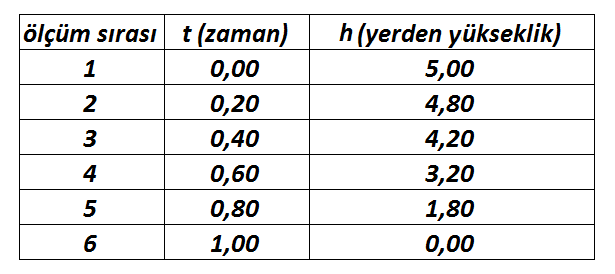
Yukarıda y ekseninden 5 metre yükseklikten kendi haline bırakılan bir cismin zamana göre yerden yüksekliğini gösteren bir tablo görmektesiniz. Bu değerlerden zaman bağımsız değişken iken, cismin yerden yüksekliği ise bağımlı değişkendir.
Tablodan da anlaşılacağı üzere zaman ilerledikçe cismin yerden yüksekliği giderek azalmakta ve 1. saniye sonunda cismimiz apsis eksenine ulaşmaktadır.
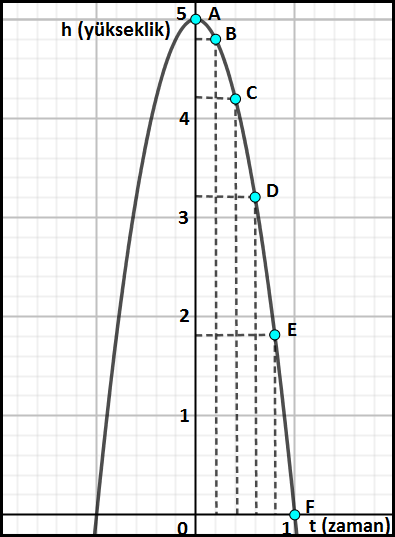
Şimdi aşağıya bu olayın grafiğini çizelim.
Yukarıdaki grafiği incelediğimizde bunun ters bir parabol olduğu hemen anlaşılır. bir parabolün genel denklemi y = a.x² + b.x + c olduğunu matematik bilgilerimizden zaten biliyoruz.
burada bağımsız değişkenimiz t olduğu için yukarıdaki denklemde x yerine t koyarız ve bağımlı değişkenimiz de h olduğu için y yerine de h koyarız.
Şimdi denklemimizi yeniden düzenleyelim.
h = a.t² + b.t + c artık işimiz a, b ve c değerlerini bulmaya kaldı.
t = 0 için h = 5 olduğunu hem tablodan hem de grafikten görebiliriz.
5 = a.0² + b.0 + c
5 = 0 + 0 + c
5 = c
c = 5 olur.
c yerine 5 koyarak denklemimizi yeniden düzenleyelim.
h = a.t² + b.t + 5
t = 1 için h = 0 olduğunu hem tablodan hem de grafikten görebiliriz.
0 = a.1² + b.1 + 5
0 = a.1 + b + 5
0 = a + b + 5
0 - 5 = a + b
-5 = a + b
a + b = -5 olur.
Son olarak ta herhangi bir ölçüm değerinin bağımsız ve bağımlı değişken değerini denklemimizde yerlerine koyalım.
Örneğin, t = 0,40 için h = 4,20 değerini kullanalım.
4,20 = a.(0,40)² + b.(0,40) + 5
4,20 = 0,16.a + 0,4.b + 5
4,20 - 5 = 0,16.a + 0,4.b
-0,8 = 0,16.a + 0,4.b
-0,8/0,16 = 0,16.a/0,16 + 0,4.b/0,16
-5 = a + 2,5.b
a + 2,5.b = -5 sonucunu elde ederiz.
a + b = -5
a + 2,5.b = -5
-(a + b) = -(-5)
a + 2,5.b = -5
-a - b = 5
+a + 2,5.b = -5
1,5.b = 0
b = 0 olarak bulunur.
a + b = -5 olduğuna göre
a + 0 = -5
a = -5 olur.
Bu değerleri h = a.t² + b.t + c denklemimizde yerine koyalım.
h = -5.t² + 0.t + 5
h = -5.t² + 0 + 5
h = -5.t² + 5 olarak bulunur.
Örneğin cismimizin t = 3. saniye anındaki konumunu bulalım.
h = -5.t² + 5
h = -5.3² + 5
h = -5.9 + 5
h = -45 + 5
h = -40 metre olarak çıkar ve bu değer bize cismimizin 3. saniye anında y ekseninin (apsis) 40 m aşağısında bulunduğunu anlatmaktadır.
Published Date:
May 01, 2020
Updated Date:
December 12, 2023