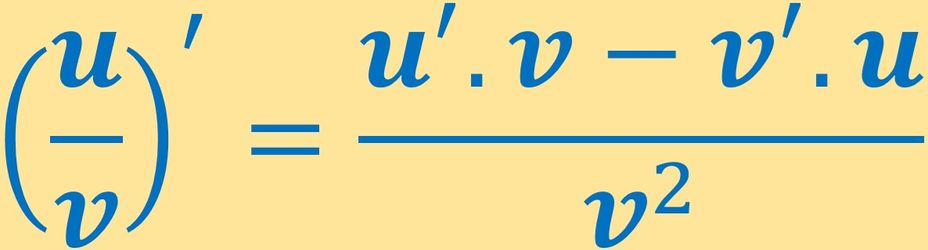[u(x)/v(x)]'=[u(x)'.v(x)-v(x)'.u(x)]/[v(x)]²'dir.
İki Fonksiyonun Bölümünün Türevi Nedir ? [ v ( x ) u ( x ) ] ′ = [ v ( x ) ] 2 u ( x ) ′ . v ( x ) − v ( x ) ′ . u ( x )
d x d [ v ( x ) u ( x ) ] = [ v ( x ) ] 2 d x d [ u ( x )] . v ( x ) − d x d [ v ( x )] . u ( x )
Bölümün Türevinin İspatı 1. Yol f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x )
[ v ( x ) u ( x ) ] ′ = h → 0 lim h v ( x + h ) u ( x + h ) − v ( x ) u ( x )
[ v ( x ) u ( x ) ] ′ = h → 0 lim h v ( x ) . v ( x + h ) u ( x + h ) . v ( x ) − v ( x + h ) . u ( x )
[ v ( x ) u ( x ) ] ′ = h → 0 lim [ h 1 . v ( x ) . v ( x + h ) u ( x + h ) . v ( x ) − v ( x + h ) . u ( x ) ]
[ v ( x ) u ( x ) ] ′ = h → 0 lim [ h . v ( x ) . v ( x + h ) u ( x + h ) . v ( x ) − v ( x + h ) . u ( x ) ]
[ v ( x ) u ( x ) ] ′ = h → 0 lim [ h . v ( x ) . v ( x + h ) u ( x + h ) . v ( x ) − v ( x + h ) . u ( x ) + u ( x ) . v ( x ) − u ( x ) . v ( x ) ]
[ v ( x ) u ( x ) ] ′ = h → 0 lim [ h . v ( x ) . v ( x + h ) u ( x + h ) . v ( x ) − u ( x ) . v ( x ) + u ( x ) . v ( x ) − v ( x + h ) . u ( x ) ]
[ v ( x ) u ( x ) ] ′ = h → 0 lim [ h . v ( x ) . v ( x + h ) u ( x + h ) . v ( x ) − u ( x ) . v ( x ) + h . v ( x ) . v ( x + h ) u ( x ) . v ( x ) − v ( x + h ) . u ( x ) ]
[ v ( x ) u ( x ) ] ′ = h → 0 lim { h . v ( x ) . v ( x + h ) v ( x ) . [ u ( x + h ) − u ( x )] + h . v ( x ) . v ( x + h ) u ( x ) . [ v ( x ) − v ( x + h )] }
[ v ( x ) u ( x ) ] ′ = h → 0 lim [ v ( x ) . v ( x + h ) v ( x ) . h u ( x + h ) − u ( x ) + v ( x ) . v ( x + h ) u ( x ) . h v ( x ) − v ( x + h ) ]
[ v ( x ) u ( x ) ] ′ = h → 0 lim v ( x ) . v ( x + h ) v ( x ) . h → 0 lim h u ( x + h ) − u ( x ) + h → 0 lim v ( x ) . v ( x + h ) u ( x ) . h → 0 lim h v ( x ) − v ( x + h )
[ v ( x ) u ( x ) ] ′ = v ( x ) . v ( x + 0 ) v ( x ) . u ′ ( x ) + v ( x ) . v ( x + 0 ) u ( x ) . − v ′ ( x )
[ v ( x ) u ( x ) ] ′ = v ( x ) . v ( x ) v ( x ) . u ′ ( x ) + v ( x ) . v ( x ) u ( x ) . − v ′ ( x )
[ v ( x ) u ( x ) ] ′ = [ v ( x ) ] 2 v ( x ) . u ′ ( x ) + [ v ( x ) ] 2 u ( x ) . − v ′ ( x )
[ v ( x ) u ( x ) ] ′ = [ v ( x ) ] 2 v ( x ) . u ′ ( x ) + [ u ( x ) . − v ′ ( x )]
[ v ( x ) u ( x ) ] ′ = [ v ( x ) ] 2 v ( x ) . u ′ ( x ) − u ( x ) . v ′ ( x )
[ v ( x ) u ( x ) ] ′ = [ v ( x ) ] 2 u ′ ( x ) . v ( x ) − v ′ ( x ) . u ( x )
2. Yol f ( x ) = v ( x ) u ( x )
l n f ( x ) = l n [ v ( x ) u ( x ) ]
l n f ( x ) = l n u ( x ) − l n v ( x )
( l n u ) ′ = u u ′
f ( x ) f ′ ( x ) = u ( x ) u ′ ( x ) − v ( x ) v ′ ( x )
f ( x ) f ′ ( x ) = u ( x ) . v ( x ) u ′ ( x ) . v ( x ) − v ′ ( x ) . u ( x )
v ( x ) u ( x ) f ′ ( x ) = u ( x ) . v ( x ) u ′ ( x ) . v ( x ) − v ′ ( x ) . u ( x )
f ′ ( x ) = v ( x ) u ( x ) . u ( x ) . v ( x ) u ′ ( x ) . v ( x ) − v ′ ( x ) . u ( x )
f ′ ( x ) = v ( x ) . v ( x ) u ′ ( x ) . v ( x ) − v ′ ( x ) . u ( x )
f ′ ( x ) = [ v ( x ) ] 2 u ′ ( x ) . v ( x ) − v ′ ( x ) . u ( x )
3. Yol y = f ( x )
y + d y = f ( x + d x )
y + d y − y = f ( x + d x ) − f ( x )
d y = f ( x + d x ) − f ( x )
d x d y = d x f ( x + d x ) − f ( x )
d x d y = d x → 0 lim d x f ( x + d x ) − f ( x )
d x d y = f ′ ( x )
d x d y = y ′
y = v u
y + d y = v + d v u + d u
y + d y − y = v + d v u + d u − v u
d y = v + d v u + d u − v u
d y = v . ( v + d v ) v . ( u + d u ) − u . ( v + d v )
d y = v 2 + v . d v v . u + v . d u − u . v − u . d v
d y = v 2 + ihmal edilir v . d v v . d u − u . d v
d y = v 2 v . d u − u . d v
d x d y = v 2 d x v . d u − d x u . d v
d x d y = v 2 v . d x d u − u . d x d v
y ′ = v 2 v . u ′ − u . v ′
y ′ = v 2 u ′ . v − v ′ . u
Soru f ( x ) = 2 x − 3 3 x + 5 ⇒ f ′ ( x ) = ?
Cevap f ′ ( x ) = ( 2 x − 3 3 x + 5 ) ′
f ′ ( x ) = ( 2 x − 3 ) 2 ( 3 x + 5 ) ′ . ( 2 x − 3 ) − ( 2 x − 3 ) ′ . ( 3 x + 5 )
f ′ ( x ) = ( 2 x − 3 ) 2 3. ( 2 x − 3 ) − 2. ( 3 x + 5 )
f ′ ( x ) = ( 2 x − 3 ) 2 3.2 x − 3.3 − 2.3 x − 2.5
f ′ ( x ) = ( 2 x − 3 ) 2 6 x − 9 − 6 x − 10
f ′ ( x ) = ( 2 x − 3 ) 2 − 19
f ′ ( x ) = − ( 2 x − 3 ) 2 19