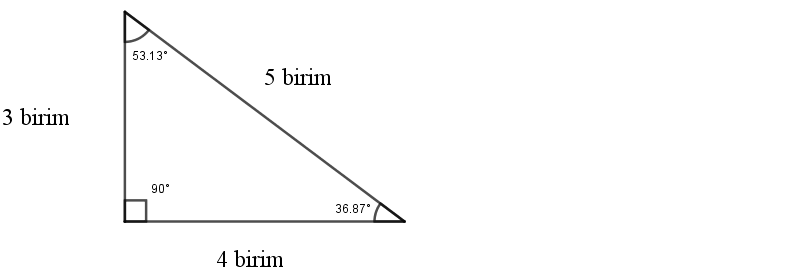
3 4 5 Üçgeni (3 4 5 Üçgeni Açıları)

Pow
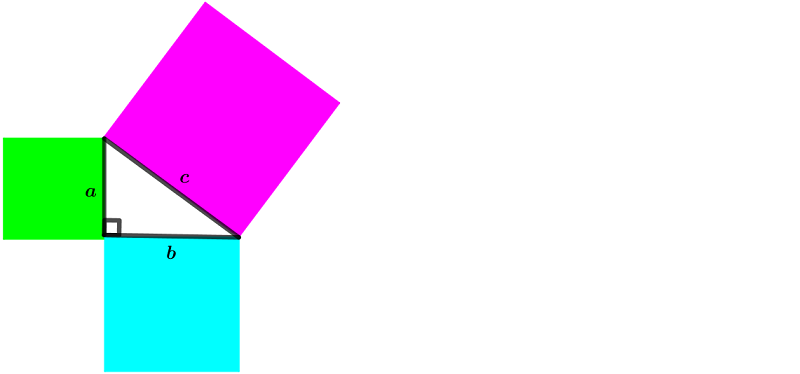
Pisagor Teoremi Yukarıdaki dik üçgende Pisagor Teoremi'ne göre; karşı dik kenar (a kenarı) ile komşu dik kenarın (b kenarı) uzunluklarının kareleri toplamı h
Pisagor Teoremi
Yukarıdaki dik üçgende Pisagor Teoremi'ne göre; karşı dik kenar (a kenarı) ile komşu dik kenarın (b kenarı) uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.
a² + b² = c²
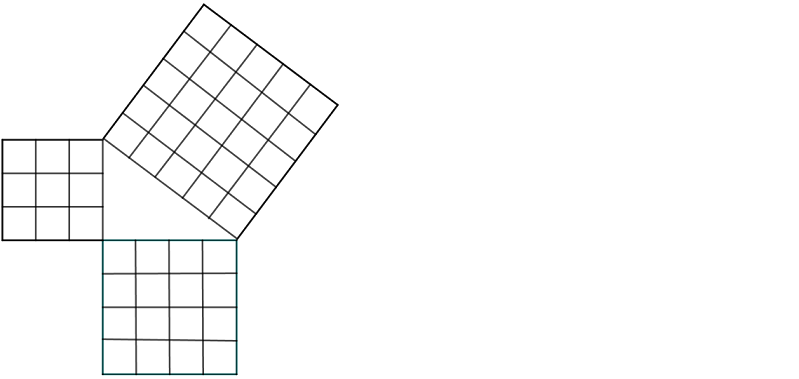
3 4 5 Üçgeni ve Özellikleri
a = 3 ve b = 4 olursa;
c² = 3² + 4²
c² = 9 + 16
c² = 25
√c² = √25
c = 5 olur.
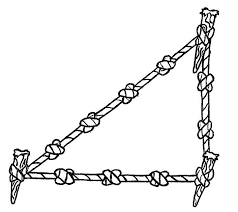
Eski Mısırlılar (M.Ö. 3150-332) ve Babilliler (M.Ö. 1895-539) kenar uzunlukları 3, 4 ve 5 birim olan bir üçgenin bir dik üçgen olduğunu biliyorlardı. Eski Mısırlılar, üzerine belli aralıklarla düğüm atılmış bir ipi cetvel olarak kullanmışlar ve kenar uzunlukları 3, 4 ve 5 birim olan bir dik üçgen elde edebilmek için de bu ipten yararlanmışlardı.
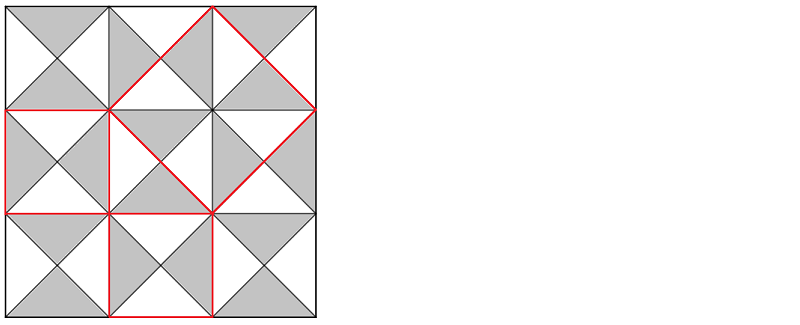
Mısırlı ve Babilli matematikçiler kenar uzunlukları 3, 4 ve 5 birim olan bir üçgenin neden bir dik üçgen olduğunu hiç merak etmemişlerdi. Eski Yunan matematikçiler ise daha çok bu konular üzerinde durdular. Eski Yunanlar'da "3, 4, 5 Üçgeni"ni biliyorlardı ve seramik yer karolarının desenlerinde başka dik üçgenlerin de olduğunu gördüler.
Yukarıdaki karo şeklindeki seramiğin desenlerine dikkatlice bakıldığında kenarları kırmızı ile belirtilmiş olan büyük karenin alanının diğer iki küçük karenin alanlarının toplamına eşit olduğu rahatlıkla görülebilir.
Eski Yunan matematikçiler kenar uzunlukları ne olursa olsun bunun bütün dik üçgenler için geçerli olduğunu anladılar. Bu eşitliği ilk kanıtlayan kişinin Öklid olduğu sanılsa da kanıt matematik dünyasında daha çok Pisagor Teoremi olarak bilinir.
3, 4, 5 veya bunun katı olan (3k, 4k, 5k) üçgenlerde kısa kenarın karşısındaki açının değeri yaklaşık olarak 37° (Gerçek Değeri 36,87°) ve uzun kenarın karşısındaki açının değeri ise yaklaşık olarak 53° (Gerçek Değeri 53,13°)'dir.
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.