f(x) = 1/x ⇒ f'(x) = -1/x²'dir.
1/x'in türevi nedir ? f ( x ) = x 1 ⇒ f ′ ( x ) = − x 2 1
1/x'in türevinin ispatı 1. Yol f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) ( x 1 ) ′ = h → 0 lim h x + h 1 − x 1 ( x 1 ) ′ = h → 0 lim h x . ( x + h ) x − ( x + h )
( x 1 ) ′ = h → 0 lim h x 2 + x . h x − x − h
( x 1 ) ′ = h → 0 lim h x 2 + x . h − h
( x 1 ) ′ = h → 0 lim − x 2 + x . h 1
( x 1 ) ′ = − x 2 + x .0 1
( x 1 ) ′ = − x 2 + 0 1
( x 1 ) ′ = − x 2 1
2. Yol f ( x ) = x 1
f ( x ) = x − 1
l n f ( x ) = l n x − 1
l n f ( x ) = − 1. l n x
l n f ( x ) = − l n x
[ l n f ( x ) ] ′ = ( − l n x ) ′
[ l n f ( x ) ] ′ = − ( l n x ) ′
f ( x ) = l n g ( x ) ⇒ f ′ ( x ) = g ( x ) g ′ ( x )
f ( x ) f ′ ( x ) = − x ( x ) ′
f ( x ) f ′ ( x ) = − x 1
f ′ ( x ) = − x 1 . f ( x )
f ′ ( x ) = − x 1 . x 1
f ′ ( x ) = − x . x 1.1
f ′ ( x ) = − x 2 1
3. Yol f ( x ) = x 1
f ( x ) . x = 1
[ f ( x ) . x ] = ( 1 ) ′
f ( x ) = u ( x ) . v ( x ) ⇒ f ′ ( x ) = u ′ ( x ) . v ( x ) + v ′ ( x ) . u ( x )
f ′ ( x ) . x + ( x ) ′ . f ( x ) = 0
f ′ ( x ) . x + 1. f ( x ) = 0
f ′ ( x ) . x + f ( x ) = 0
f ′ ( x ) . x = − f ( x )
f ′ ( x ) = − x f ( x )
f ′ ( x ) = − x x 1
f ′ ( x ) = − 1 x x 1
f ′ ( x ) = − x 1 . x 1
f ′ ( x ) = − x . x 1.1
f ′ ( x ) = − x 2 1

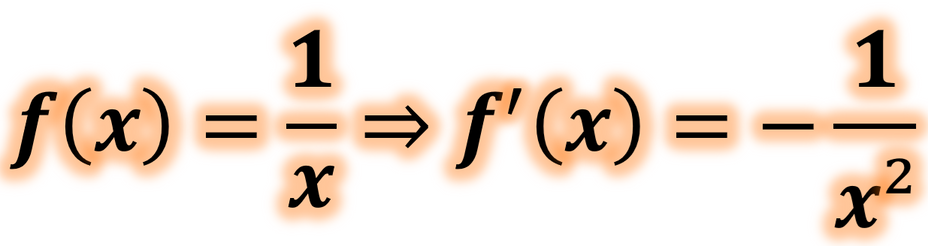 1/x'in türevi nedir ?
1/x'in türevi nedir ?