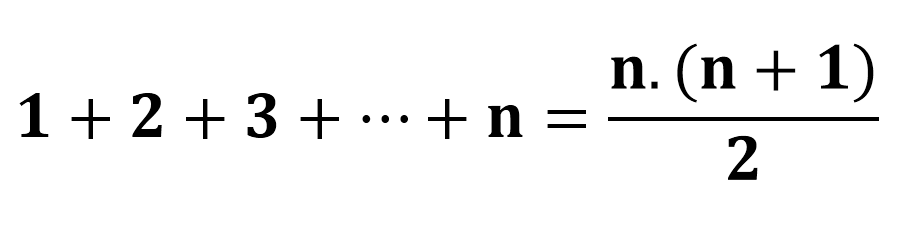1 + 2 + 3 + ... + n = n.(n + 1)/2'in İspatı

Pow
1 + 2 + 3 + ... + n dizisinin toplamının n.(n + 1)/2'ye eşit olduğunu çok çeşitli yollardan ispatlayabiliriz. Aşağı da bu yollardan birkaç tanesini gösterdi
1 + 2 + 3 + ... + n dizisinin toplamının n.(n + 1)/2'ye eşit olduğunu çok çeşitli yollardan ispatlayabiliriz. Aşağı da bu yollardan birkaç tanesini gösterdik.
1.Yol
2. Yol
3. Yol
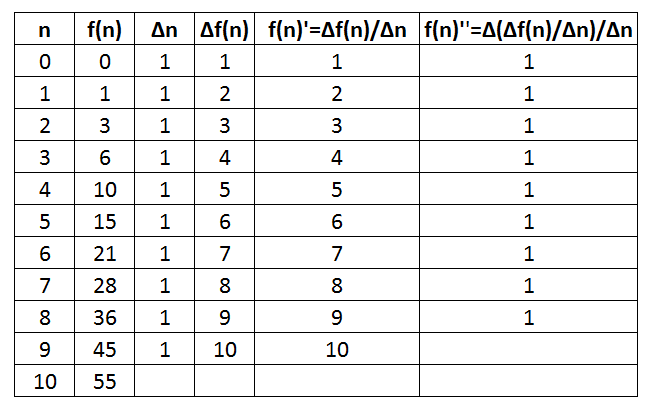
Yukarıdaki tablonun 5. sütununda fonksiyonumuzun belirli aralıklardaki ortalama değişim oranlarını (hızlarını) görmektesiniz. Örneğin; 0 ile 1 aralığındaki değişim oranı 1, 4 ile 5 aralığındaki değişim oranı 5 ve 8 ile 9 Aralığındaki değişim oranı ise 9’dur. Anlık değişim oranlarını bulmak istersek eğer fonksiyonumuzun türevini almamız gerekir.
Tablomuzun 6. sütununda ise fonksiyonumuzun belirli bir aralıktaki ortalama değişim oranının ortalama değişim oranını görmektesiniz. Ancak bu değer sabit ve 1’e eşittir. Anlık değişim oranının anlık değişim oranını bulmak istersek eğer bu sefer fonksiyonumuzun 2. türevini almamız gerekir.
Matematikte bir fonksiyonun türevi sabit bir sayıya eşit ise eğer bu fonksiyon a.x+b şeklinde bir fonksiyondur. Örneğin;
f(x)=3.x+5 fonksiyonun türevini ele alalım f(x)'=3'tür.
Yukarıdaki f(n) fonksiyonunun, birinci türevi f(n)’ ve ikinci türevi f(n)’’ şeklinde gösterilir.
4. Yol
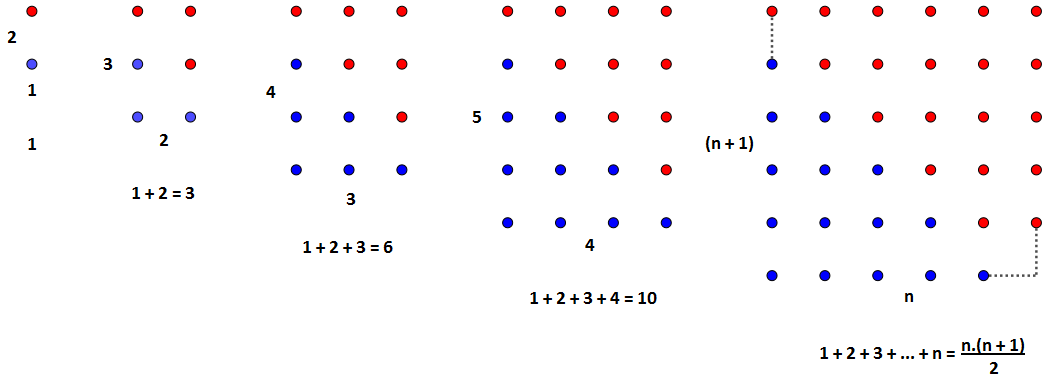
Yukarıdaki şekillerin her birinde mavi noktaların sayısı kırmızı noktaların sayısına eşittir.
1. Şekildeki mavi nokta sayısı = (1 x 2)/2 = 2/2 = 1
2. Şekildeki mavi nokta sayısı = (2 x 3)/2 = 6/2 = 3
3. Şekildeki mavi nokta sayısı = (3 x 4)/2 = 12/2 = 6
4. Şekildeki mavi nokta sayısı = (4 x 5)/2 = 20/2 = 10
5. Şekildeki mavi nokta sayısı = n x (n +1)/2
Share Your Expertise, Earn Rewards!
Found this insightful? Imagine your knowledge generating income. Contribute your articles to bylge.com and connect with readers while unlocking your earning potential.