Üçgenin İç Açıları Toplamı (Üçgenin İç Açıları Toplamı Kaçtır?)
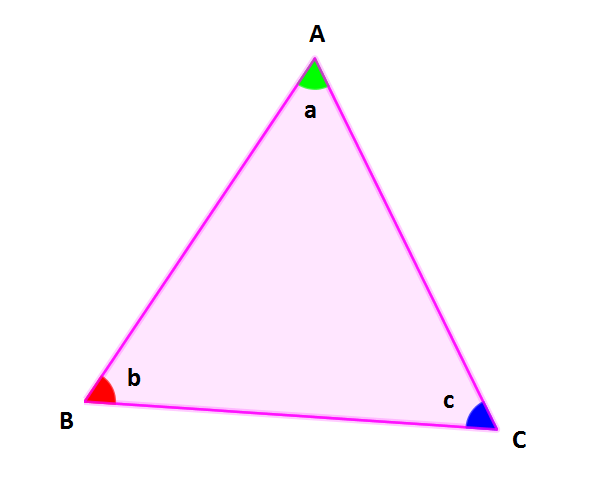
Üçgenin İç Açıları Toplamı Neden 180 Derecedir? Bir üçgenlerde iç açıların toplamı 180°'dir. Yukarıdaki ABC üçgeninde; m (A) + m (B) + m (C) = a + b + c = 18

Pow
@powÜçgenin İç Açıları Toplamı Neden 180 Derecedir?
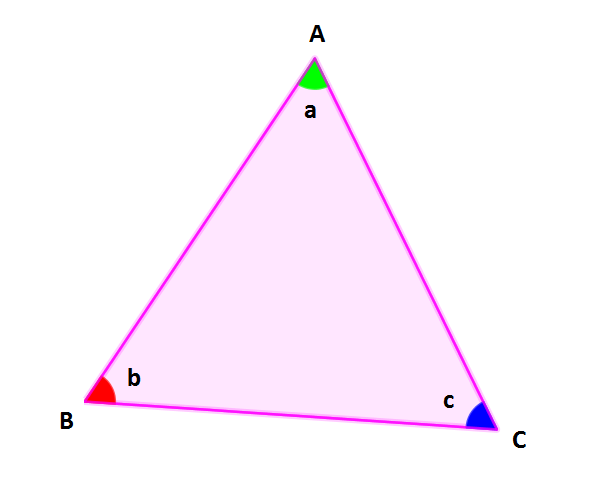
Bir üçgenlerde iç açıların toplamı 180°'dir. Yukarıdaki ABC üçgeninde;
m (A) + m (B) + m (C) = a + b + c = 180° olur.
Bir üçgenin iç açılarının toplamının 180° olduğunu çeşitli yollardan ispatlayabiliriz.
1. Yol
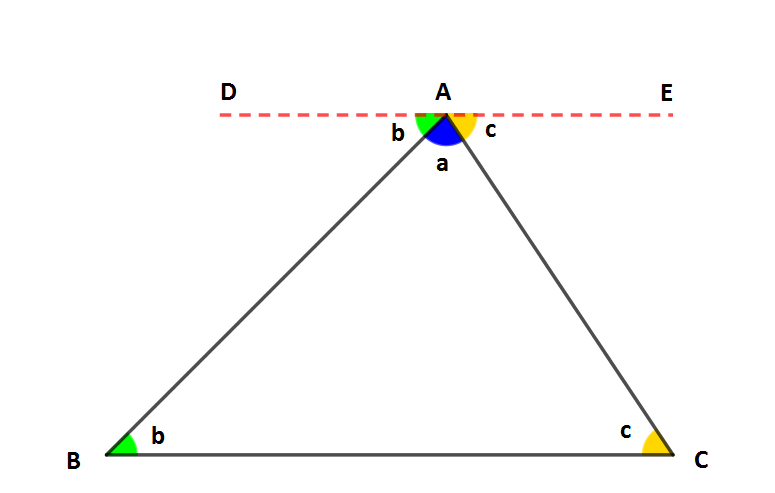
Yukarıdaki ABC üçgeninde kırmızı kesikli çizgiler ile gösterdiğimiz DE doğru paçası BC kenarına paraleldir.
Yani; [DE] // |BC|'dir.
Geometri derslerinde açı konusunu işlerken öğrendiğimiz bilgilere göre DAB ile ABC ve EAC ile BCA açıları iç ters açılardır. Hepimizin bildiği üzere iç ters açıların ölçüleri birbirine eşittir.
Yani; m (DAB) = m (ABC) = b ve m (EAC) = m (BCA) = c olur.
şekildeki DAE doğru parçası üzerinde oluşan açı bir doğru açıdır ve bir doğru açının ölçüsü de 180°'dir.
m (DAE) = 180 = b + a + c = a + b + c olur.
(a + b + c)'nin toplamı olan 180 üçgenin iç açılarının toplamına eşittir.
Böylelikle bir üçgenin iç açılarının toplamının 180 derece olduğunu bu şekilde ispatlamış olduk.
2. Yol
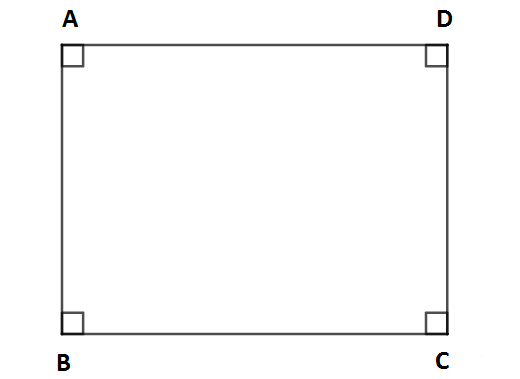
Yukarıdaki ABCD dikdörtgeninde A ve C veya B ve D köşelerini birleştiren bir doğru parçası çizelim. Biz B ve D köşelerini birleştiren bir doğru parçası çizmeye tercih ettik.
[BD] doğru parçası dikdörtgeni ikiye ayırarak ABD ve BCD olmak üzere iki tane üçgen oluşmasını sağlar.
ABD üçgenin iç açılarını toplamı:
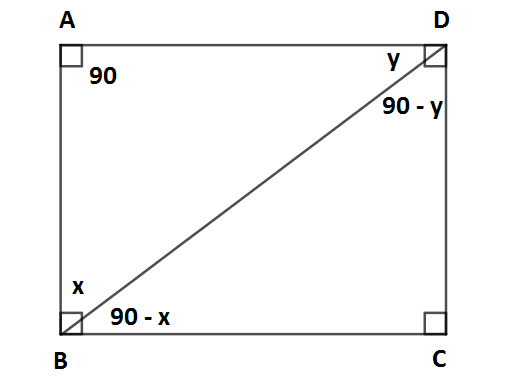
m (A) + m (B) + m (D) = 90 + x + y (1. Denklem)
BCD üçgenin iç açılarını toplamı:
m (B) + m (C) + m (D) = 90 - x + 90 + 90 - y = 90 + 90 + 90 - x - y = 270 - (x + y) (2. Denklem)
[AD] doğru parçası [BC] doğru parçasına paralel olduğu için [AD] // [BC]
m (ADB) = m (DBC) ve y = 90 - x olur.
1. Denklem de y gördüğümüz yere 90 - x yazalım.
m (A) + m (B) + m (D) = 90 + x + y
m (A) + m (B) + m (D) = 90 + x + 90 - x
m (A) + m (B) + m (D) = 90 + 90 + x - x
m (A) + m (B) + m (D) = 180 + 0 = 180 olur.
Gerçekten de ABD üçgenin iç açılarını toplamı 180° olarak çıktı.
Şimdi de 2. denklemimiz de y gördüğümüz yere 90 - x yazalım.
m (B) + m (C) + m (D) = 270 - (x + y)
m (B) + m (C) + m (D) = 270 - (x + 90 - x)
m (B) + m (C) + m (D) = 270 - (x - x + 90)
m (B) + m (C) + m (D) = 270 - (0 + 90)
m (B) + m (C) + m (D) = 270 - (90)
m (B) + m (C) + m (D) = 270 - 90
m (B) + m (C) + m (D) = 180
Gerçekten de BCD üçgenin iç açılarını toplamı 180° olarak çıktı.
3. Yol
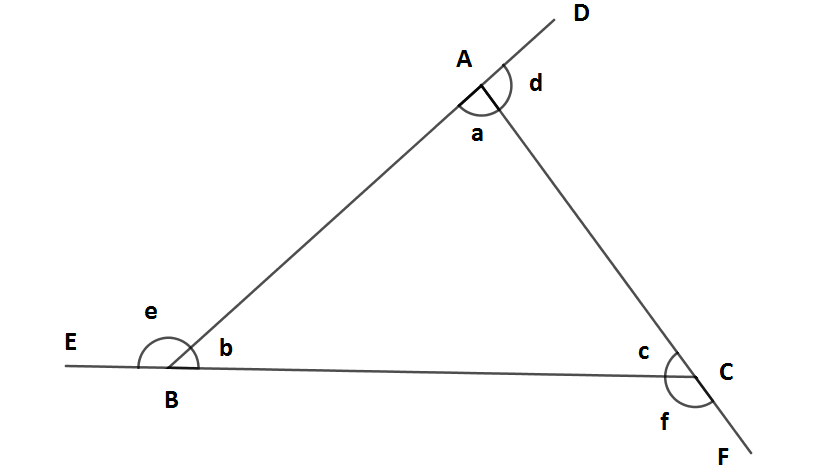
Yukarıdaki ABC üçgeninde üç tane doğru açı bulunmaktadır. Doğru açı hepinizin geometri derslerinden bildiği üzere bir doğru üzerinde bulunan ve ölçüsü 180° olan açıdır.
Birde şunu hatırlatmakta fayda var bütün çokgenlerin üçgen, dörtgen, beşgen, altıgen v.b. hepsinin dış açılarının toplamı her zaman için 360°'dir.
Şimdi ispatımıza geçelim.
a + d = 180
b + e = 180
c + f = 180
d + e + f = 360 (dış açıların toplamı)
(a + d) + (b + e) + (c + f) = 180 + 180 + 180 = 540
(a + b + c) + (d + e + f) = 540
(a + b + c) + 360 = 540
a + b + c = 540 - 360
a + b + c = 180 (iç açıların toplamı)
4. Yol
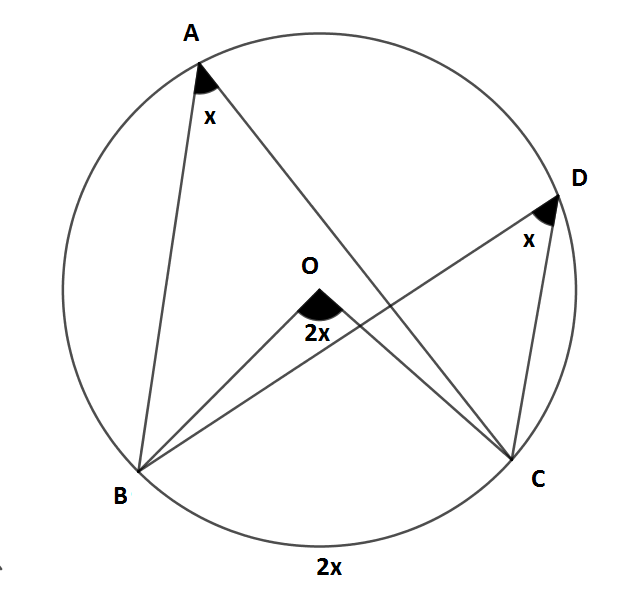
Bir çemberde merkez açı gördüğü yayın ölçüsüne ve çevre açı da gördüğü yayın ölçüsünün yarısına eşittir.
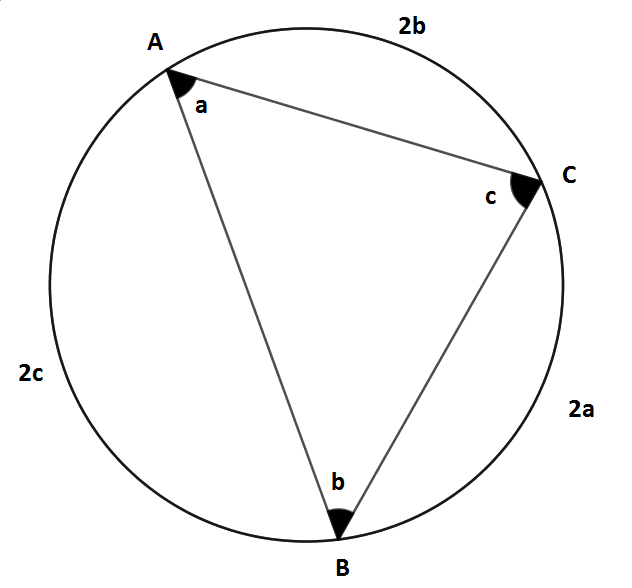
Yukarıdaki çemberde;
m (A) = a, m (B) = b, m (C) = c ve m (BC) = 2a, m (CA) = 2b, m (AB) = 2c'dir.
Şimdi tüm yayların ölçülerini toplayalım
m (BC) + m (CA) + m (AB) = 2a + 2b + 2c olur.
Tam bir çember yayının ölçüsü 360°'dir.
O zaman;
2a + 2b + 2c = 360
2.(a + b + c) = 360
a + b + c = 360/2
a + b + c = 180 olur.
Görüldüğü gibi üçgenimizin iç açıları toplamı (a + b + c) 180 derece olarak bulunur.
5. Yol
Bu yöntem göre bir defter veya kağıda çizeceğim üçgenin iç açılarını kesip birleştirmektir.
Yukarıdaki ABC üçgeninde A, B ve C açılarını kesip birleştirelim.
Yukarıdaki şekilde de görüleceği gibi kestiğimiz üç parçayı bir araya getirdiğimizde bir doğru açı oluşmaktadır.
Published Date:
May 01, 2020
Updated Date:
December 11, 2023