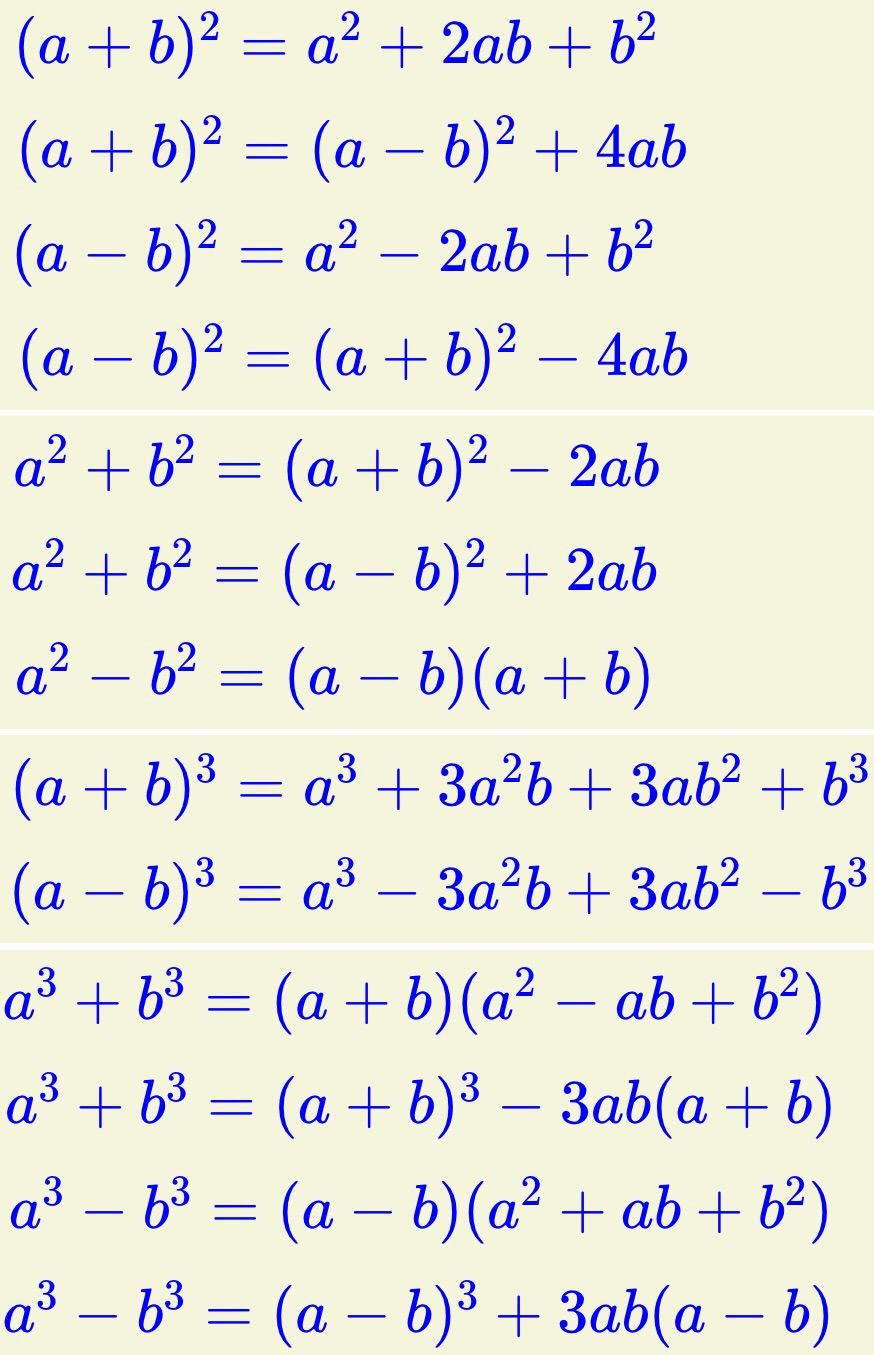Çarpanlara Ayırma Formülleri

Çarpanlara Ayırma Formülleri

Çarpanlara Ayırma Nedir ?

Harfli bir ifadeyi iki veya daha fazla sayıda ifadenin çarpımı şeklinde yazma işlemine çarpanlara ayırma denir.

Çarpanlara Ayırma Yöntemleri

1. Ortak Çarpan Parantezine Alma

Harfli ifadeyi oluşturan terimlerin içerisinde eğer ortak bir çarpan varsa, bu harfli ifade ortak çarpan parantezi şeklinde yazabilir.

Örneğin ax + bx harfli ifadesini oluşturan terimler için x ortak bir çarpandır. İfadeyi x ortak çarpan olacak şekilde yazalım.

ax + bx = x.(a + b) olur.

İspatı

$ax=\underset{\text{a tane x}}{\underbrace{x+x+...+x}}$

$bx=\underset{\text{b tane x}}{\underbrace{x+x+...+x}}$

$ax+bx=\underset{\text{a tane x}}{\underbrace{(x+x+...+x)}}+\underset{\text{b tane x}}{\underbrace{(x+x+...+x)}}$

$ax+bx=\underset{\text{a+b tane x}}{\underbrace{x+x+...+x+x+x+...+x}}$

$ax+bx=(a+b).x$

$ax+bx=x.(a+b)$ olur.

2. Gruplandırma

Verilen çok terimli bir harfli ifadenin her teriminde ortak bir çarpan yoksa, terimler ikişerli, üçerli veya daha fazla olacak şekilde gruplara ayrılarak bu gruplar içerisinden bir ortak çarpan bulunmaya çalışılır.

Örneğin, x² + ax + bx + ab harfli ifadesinde bütün terimler için bir ortak çarpan yoktur. Bu harfli ifadeyi ancak gruplandırma yöntemi ile çarpanlarına ayırabiliriz.

x² + ax + bx + ab = (x² + ax) + (bx + ab)

x² + ax + bx + ab = x.(x + a) + b.(x + a)

x² + ax + bx + ab = (x + b).(x + a) olur.

3. İki Terim Toplamının Karesi

(a + b)² = a² + 2ab + b²

İspatı

Çarpma işlemin toplama işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki eşitliğin ispatını yapabiliriz.

$(a+b{)}^2=(a+b).(a+b)$

$(a+b{)}^2=(a+b).a+(a+b).b$

$(a+b{)}^2=a.(a+b)+b.(a+b)$

$(a+b{)}^2=a.a+a.b+b.a+b.b$

$(a+b{)}^2=a.a+a.b+a.b+b.b$

$(a+b{)}^2=a^2+2.a.b+b^2$

4. İki Terim Farkının Karesi

(a - b)² = a² - 2ab + b²

İspatı

Çarpma işlemin çıkarma işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki eşitliğin ispatını yapabiliriz.

$(a-b{)}^2=(a-b).(a-b)$

$(a-b{)}^2=(a-b).a-(a-b).b$

$(a-b{)}^2=a.(a-b)-b.(a-b)$

$(a-b{)}^2=a.a-a.b-b.a-b.-b$

$(a-b{)}^2=a^2-a.b-b.a+b^2$

$(a-b{)}^2=a^2-a.b-a.b+b^2$

$(a-b{)}^2=a^2-2.a.b+b^2$

5. İki Terim Toplamının Küpü

(a + b)³ = a³ + 3a²b + 3ab² + b³

İspatı

Çarpma işlemin toplama işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki eşitliğin ispatını yapabiliriz.

$(a+b{)}^3=(a+b{)}^2.(a+b)$

$(a+b{)}^2=a^2+2.a.b+b^2$ (Bu eşitliği daha önceden bulmuştuk)

Şimdi bu değeri üstteki eşitlikte yerine koyalım.

$(a+b{)}^3=(a^2+2.a.b+b^2).(a+b)$

$(a+b{)}^3=(a^2+2.a.b+b^2).a+(a^2+2.a.b+b^2).b$

$(a+b{)}^3=a.(a^2+2.a.b+b^2)+b.(a^2+2.a.b+b^2)$

$(a+b{)}^3=a.a^2+a.2.a.b+a.b^2+b.a^2+b.2.a.b+b.b^2$

$(a+b{)}^3=a^3+2.a^2.b+a.b^2+b.a^2+2.a.b^2+b^3$

$(a+b{)}^3=a^3+2.a^2.b+a.b^2+a^2.b+2.a.b^2+b^3$

$(a+b{)}^3=a^3+3.a^2.b+3.a.b^2+b^3$

6. İki Terim Farkının Küpü

(a - b)³ = a³ - 3a²b + 3ab² - b³

İspatı

Çarpma işlemin çıkarma işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki eşitliğin ispatını yapabiliriz.

$(a-b{)}^3=(a-b{)}^2.(a-b)$

$(a-b{)}^2=a^2-2.a.b+b^2$ (Bu eşitliği daha önceden bulmuştuk)

Şimdi bu değeri üstteki eşitlikte yerine koyalım.

$(a-b{)}^3=(a^2-2.a.b+b^2).(a-b)$

$(a-b{)}^3=(a^2-2.a.b+b^2).a-(a^2-2.a.b+b^2).b$

$(a-b{)}^3=a.(a^2-2.a.b+b^2)-b.(a^2-2.a.b+b^2)$

$(a-b{)}^3=a.a^2-a.2.a.b+a.b^2-b.a^2-b.-2.a.b-b.b^2$

$(a-b{)}^3=a^3-2.a^2.b+a.b^2-b.a^2+2.a.b^2-b^3$

$(a-b{)}^3=a^3-2.a^2.b+a.b^2-a^2.b+2.a.b^2-b^3$

$(a-b{)}^3=a^3-3.a^2.b+3.a.b^2-b^3$

7. İki Terim Küpünün Toplamı

a³ + b³ = (a + b).(a² - ab + b²)

1. İspatı

$a^3+3.a^2.b+3.a.b^2+b^3=(a+b{)}^3$

$a^3+b^3=(a+b{)}^3-3.a^2.b-3.a.b^2$

$a^3+b^3=(a+b{)}^3-3.a.b.(a+b)$

$a^3+b^3=(a+b{)}^2.(a+b)-3.a.b.(a+b)$

$a^3+b^3=(a^2+2.a.b+b^2).(a+b)-3.a.b.(a+b)$

$a^3+b^3=(a^2+2.a.b+b^2-3.a.b).(a+b)$

$a^3+b^3=(a^2-a.b+b^2).(a+b)$

$a^3+b^3=(a+b).(a^2-a.b+b^2)$

2. İspatı

Polinomlarda bölme işlemi kurallarından faydalanarak da ispatını yapabiliriz.

$\frac{a^3+b^3}{a+b}=a^2-ab+b^2$

$a^3+b^3=(a+b).(a^2-ab+b^2)$ olur.

8. İki Terim Küpünün Farkı

a³ - b³ = (a - b).(a² + ab + b²)

1. İspatı

$a^3-3.a^2.b+3.a.b^2-b^3=(a-b{)}^3$

$a^3-b^3=(a-b{)}^3+3.a^2.b-3.a.b^2$

$a^3-b^3=(a-b{)}^3+3.a.b.(a-b)$

$a^3-b^3=(a-b{)}^2.(a-b)+3.a.b.(a-b)$

$a^3-b^3=(a^2-2.a.b+b^2).(a-b)+3.a.b.(a-b)$

$a^3-b^3=(a^2-2.a.b+b^2+3.a.b).(a-b)$

$a^3-b^3=(a^2+a.b+b^2).(a-b)$

$a^3-b^3=(a-b).(a^2+a.b+b^2)$

2. İspatı

Polinomlarda bölme işlemi kurallarından faydalanarak da ispatını yapabiliriz.

$\frac{a^3-b^3}{a-b}=a^2+ab+b^2$

$a^3-b^3=(a-b).(a^2+ab+b^2)$ olur.

9. İki Terim Karesinin Toplamı

a² + b² = (a + b)² - 2ab

a² + b² = (a - b)² + 2ab

10. İki Terim Karesinin Farkı

a² - b² = (a + b).(a - b)

İspatı

Çarpma işlemin toplama ve çıkarma işlemi üzerindeki dağılma özelliğinden faydalanarak yukarıdaki eşitliğin ispatını yapabiliriz.

$(a-b).(a+b)=(a-b).a+(a-b).b$

$(a-b).(a+b)=a.(a-b)+b.(a-b)$

$(a-b).(a+b)=a.a-a.b+b.a-b.b$

$(a-b).(a+b)=a.a-\cancel{a.b}+\cancel{a.b}-b.b$

$(a-b).(a+b)=a.a-b.b$

$(a-b).(a+b)=a^2-b^2$

11. Üç Terim Toplamının Karesi

(a + b + c)² = a² + b² + c² + 2(ab + ac + bc)

İspat

$(a+b+c{)}^2=(a+b+c).(a+b+c)$

$(a+b+c{)}^2=(a+b+c).a+(a+b+c).b+(a+b+c).c$

$(a+b+c{)}^2=a.(a+b+c)+b.(a+b+c)+c.(a+b+c)$

$(a+b+c{)}^2=a.a+a.b+a.c+b.a+b.b+b.c+c.a+c.b+c.c$

$(a+b+c{)}^2=a.a+a.b+a.c+a.b+b.b+b.c+a.c+b.c+c.c$

$(a+b+c{)}^2=a.a+b.b+c.c+a.b+a.b+a.c+a.c+b.c+b.c$

$(a+b+c{)}^2=a^2+b^2+c^2+2.a.b+2.a.c+2.b.c$